Integralrechnung, Polynomdivison , PQ formel usw.?
Hallo , ich habe ein Problem mit der Aufgabe 4c , den Rest hab ich verstanden.
Wie muss ich das berechnen?
fx=0?
Aber das würde ja kein Sinn ergeben ?
Dann kann ich ja nichts umformen und die Null kann ich ja auch nicht für x einsetzen weil es ein y wert ist
Ich bitte um dringende Hilfe
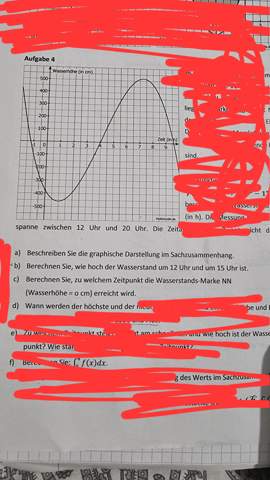
Die Funktion lautet f(x)= -8x³+99x²-174x-376
4 Antworten
Erste Nullstelle bei x = 4 "vermuten" (Graph) und durch Rechnung bestätigen. Dann Polynomdivision und pq-Formel.
Wie muss ich das berechnen?
fx=0?
Ja.
0 = -8x³+99x²-174x-376
Nullstelle bei x=4 ablesen, dann Polynomdivision, dann PQ
f(x)=0 ist richtig
du kannst die Nullstellen aber auch aus dem Schaubild ablesen, berechnen dürfte wohl schwieriger sein. Die erste Lösung muss man durch Probieren finden, dann Polynomdivision danach dann pq-Formel
simmt
in BW wird aber Polynomdivision schon lange nicht mehr behandelt. So eine Aufgabe wäre für Abiturienten also unlösbar
In Bayern schon, gebe im Bereich Mathematik ab und zu Nachhilfe für Abiturienten und da ist Polynomdivison standart, oder sollte es zumindest sein.
in Bayern wird noch etwas mehr gelernt, früher war das in BW auch noch üblich. Seit Einführung des G8 wurde der Lehrplan sehr ausgedünnt
Bist du dir da sicher? Würde ja bedeuten, dass man nur Polynome zweiten Grades lösen kann, oder, durch Substituieren Funktionen höheren Grades. Und das ist ja nun wirklich nicht so schwer.
Ah ok, scheinst dich ja was das angeht auszukennen, wusste ich gar nicht das es da so signifikante Unterschiede gibt, danke für die Aufklärung :D
höhere Polynome nur durch Ausklammern (dann hat f also keine Konstante) oder durch Substitution bei biquadratischen
Das hat überhaupt nichts mit Integralrechnung zu tun.
Du musst wie folgt vorgehen:
f(x)= -8x³+99x²-174x-376 ist das gleiche wie y= -8x³+99x²-174x-376.
Setzte also für y 0 ein, dann kannst du erst eine Polynomdivision durchführen. Dann hast du eine Funktion 2. Grades und kannst die pq-Formel anwenden.
PS: Bei der Integralrechung bestimmt man Flächeninhalte von Funktionen zwischen Bereichen x bis y und das ganze dann bis zur Abszissen Achse als grenze
Aufgabe lautet: *Berechne*. Ablesen wäre aber auch Grundschul Niveau :D