Hilfe beim Ausklammern?
Hallo,
ich frage mich, wie man aus dem Term
E = (m₀/√(1 − v²/c²))∙c² − m₀c²
den Term
E = m₀∙c²∙(1/√(1 − v²/c²) − 1)
macht. Ich denke, dass hier einfach ausgeklammert wurde, verstehe aber nicht ganz, wie man auf die -1 im 2. Term kommt.
Vielen Dank
Für einfacheres Verständnis auch noch mal ein Bild der Gleichungen:
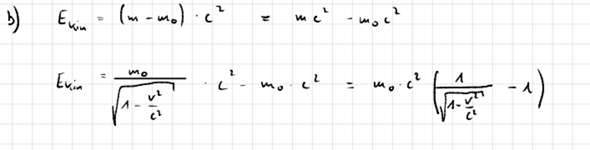
4 Antworten
Ja, es wurde m0*c^2 ausgeklammert. Wenn du das ganze ausmultiplizierst siehst du, woher die -1 kommt (sie kommt von dem rechten Summanden, also von m0*c^2)
Ah macht Sinn,
so dumm es sich auch anhören mag, habe ich einfach falsch ausmultipliziert und jeweils für eine 1 eine Variable eingesetzt, was ja offensichtlich falsch ist.
Also vielen Dank für die schnelle und gute Hilfe
Hallo Khonsument,
im zweiten Term steht vor dem Ausklammern "− m₀c²", und da m₀c² ausgeklammert wird, bleibt dort nach dem Ausklammern eben "− 1" übrig.
AbkürzungenIn der Speziellen Relativitätstheorie (SRT), zu der ja diese Aufgabe gehört, sind die Abkürzungen
(1.1) β := v⁄c
und
(1.2) γ := 1/√{1 − β²}
üblich; γ heißt auch der LORENTZ- Faktor.
Damit lässt sich der Ausdruck für die kinetische Energie übersichtlicher schreiben:
(1.3) Eₖ = m₀γc² − m₀c² = m₀c²(γ − 1)
NEWTONsche NäherungWir kennen aus der NEWTONschen Mechanik (NM) einen anderen Ausdruck:
(2.1) Eₖ = ½m₀v²
Der ist zwar offensichtlich "falsch", aber bei v << c (respektive β << 1) muss das eine gute Näherung sein.
Für eine Größe x << 1 gibt es zwei Näherungen:
- √{1 − x} ≈ 1 − ½∙x
- 1/(1 − x) ≈ 1 + x
Wenn β << 1 ist, ist β² das erst recht, und wir können beide Näherungen gleichzeitig ohne nennenswerten Fehler anwenden:
(2.2) γ = 1/√{1 − β²} ≈ 1 + ½β²
und damit
(2.3) γ − 1 ≈ ½β².
Dies in (1.3) eingesetzt ergibt
(2.4) Eₖ ≈ ½β²m₀c² = ½m₀(βc)²,
was dasselbe ist wie (2.1), was wir zeigen wollten.
"Massenzunahme"EINSTEINs berühmte Gleichung
(3) E = mc²
bedeutet zweierlei:
- Masse ist nichts anderes als gleichsam kondensierte Energie.
- Jede Energie – so auch kinetische – "wiegt was".
In den Anfängen der SRT hat man die von dem Körper oder Teilchen sozusagen mitgeschleppte kinetische Energie seiner Masse zugerechnet, aber außerhalb der Schule tut das heutzutage fast niemand mehr.
-- Baustelle --
Die Idee der Massenzunahme kommt daher, dass der Impulserhaltungssatz gültig bleiben soll, und zwar unabhängig von der Wahl des Bezugssystems. Der Betrag des Impulses bzw. der 1D-Impuls p ist
(3.1) p = m₀v/√{1 − v²⁄c²} =: m₀γv,
was man zunächst als
(3.2) p = (m₀γ)v =: mₚv = mₚ∙ds⁄dt,
wobei mₚ die Impulsmasse heißt. Mit ds ist ein kleines Wegstück und mit dt eine kurze Zeitspanne nach auf einer Bezugsuhr U gemeint, die U- Koordinatenzeit.
Man kann es aber auch als
(3.3) p = m₀(γv) = m₀∙ds⁄dτ
lesen, wobei ds wieder die kurze Wegstrecke ist, dτ aber die zugehörige Zeitspanne auf einer mitgeführten Uhr Ώ, die Eigenzeit.
In der englischsprachigen
Ist doch ganz einfach: mo/irgendwas * c² = (mo*c²)/irgendwas...
jetzt klarer?
Einfach so:
a·b - a = a·(b - 1)
Anmerkung: Geändert, damit niemand auf die Idee kommt dass mein zuvor verwendetes "c" irgendwas mit der Lichtgeschwindigkeit aus der Frage zu tun hätte.