Gedämpfte Schwingung Mathematik?
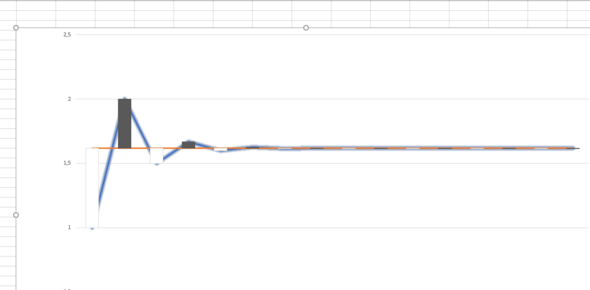
Hey, ich habe eine Funktion (blau), die sich einer anderen Funktion (orange) annähert. Ich möchte dieses Verhalten beschreiben. Nun ist es aber so, dass eine Annäherung auch, wie bspw. bei einer Exponentialfunktion, sich nur aus einer Richtung annähern kann. Meine Funktionen "schwingen" aber, sprich sie nähert sich aus "beiden Richtungen" an (ganz ähnlich einer gedämpften Schwingung in der Physik). Gibt es dafür einen mathematische Ausdruck?
5 Antworten
Also:
- Zuerst hast du den Sinus (symmetrisch, um Nulllinie herum, blau)
- Dieser muss mit einem abnehmenden Faktor multipliziert werden, damit sie sich der Nullinie nähert. Dieser Faktor kann linear abnehmen, oder eben wie eine abnehmende Exponentialfunktion bei einer realen abnehmenden Schwingung -> grün.
- Am Schluss addierst du jenen Betrag dazu, den du als Endwert willst, um den also der abklingende Sinus pendelt -> rot
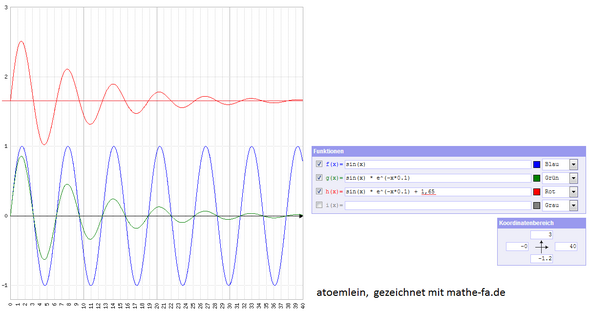
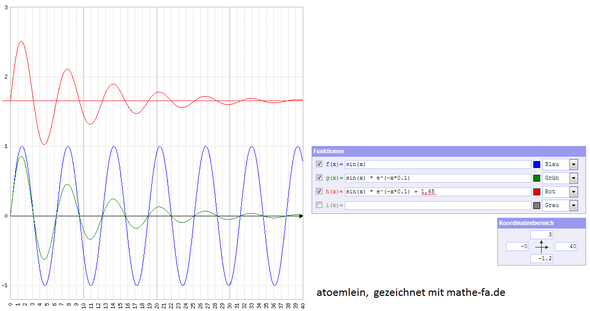
Wenn die Amplitude gegen 0 geht: Asymptote (als Funktionsgraph), Grenzwert / (anziehender) Fixpunkt (als Wert).
Wenn du die (in y-Richtung verschobenen) Exponentialfunktionen meinst, zwischen denen die Schwingungsfunktion liegt: Einhüllende (sowohl als Graph als auch als Funktion).
Im Internet habe ich zwei verschiedene Definitionen von Asymptote gefunden - einmal mit beliebig vielen Schnittpunkten (Wikipedia), das andere Mal ohne gemeinsame Punkte bzw mit beschränkter gemeinsamer Punktmenge (Onlinemathe)
(die ersten beiden Treffer von https://www.google.com/search?q=Definition+Asymptote&ie=utf-8&oe=utf-8&client=firefox-b )
Hey!
Wie viel Kenntnisse hast du zum Thema "Gedämpfte Schwingungen"?
Für mich schaut es aus wie der aperiodische Grenzfall (kann mich auch täuschen).
Der Wert der Amplitude sinkt, wegen der Dämpfung, sehr stark und die Amplitude nähert sich der orangenen Kurve an. Kannst auch mehr dazu hier lesen: https://de.m.wikipedia.org/wiki/Aperiodischer_Grenzfall
Sag bescheid, ob du dir etwas daraus basteln kannst. Wenn nicht, erzähle ich dir mehr dazu.
LG
Ach so, dann nehme ich meine Aussage zurück. Aperiodischer Grenzfall tritt bei gedämpften Schwingungen auf und ist eher eine physikalische Beschreibung. Daher weiß ich die Antwort auf deine Frage nicht...
Okay, das sieht ganz gut aus, aber ich bin mir nicht sicher, ob es das ist. Konkret geht es darum, dass sich das Verhältnis zweier aufeinanderfolgenden Fibonacci-Zahlen dem goldenen Schnitt annähert (hier meine Werte, wobei f(n) die n-te Fibonaccizahl ist: https://i.gyazo.com/7f855c5ac17b9767f83f7efbc3af369b.png ) Kannst du mir sagen, ob das ein aperiodische Grenzfall ist?
Lösung der "freien gedämpften Schwingung"
S(t)=e^(-b*t)*K*sin(w*t+c)
Der Graph ist hier nur nach oben verschoben
also S(t)=e^(-b*t)*K*sin(w*t+c)+d
K ist di Amplitude
d aus der Zeichnung ablesen ist etwas über 1.5
b ist die Abklingkonstante
c verschiebt auf der x-Achse nach "links" oder "rechts"
y1max/y2max=e^b*(t2-t1)
y1max 1.te Maximum
y2max 2.te Maximu (folgt auf y1max)
w=Wurzel(wo^2-b^2)
Differentialgleichung Dgl. y´´+2*b*y`+wo^2*y=0
Die Amplitude nähert sich an
Mein Graph hat aber keine Asymptote, die er nicht berührt, sondern eine, um die eher immer knapper schwingt (siehe Bild)