Flächenwert berechnen?
Gesucht ist der Inhalt des im Folgenden markierten Flächenstücks.
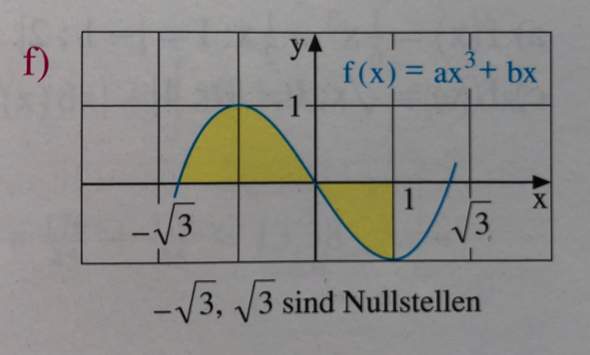
Gibt es einen ganz einfachen Weg um diese Aufgabe zu lösen? Ich kenne die Lösung dieser Aufgabe bereits, allerdings war mir der Rechenweg zu kompliziert und ich würde mich über einen sehr einfachen und verständlichen Lösungsweg dieser Aufgabe freuen.
3 Antworten
wie findet man a und b ?
.
Zwei Möglichkeiten A und B
.
A)))))
man braucht noch f'(x) = 3ax² + b
.
man weiß , dass bei -1 und +1 Extrema sind . Da ist die erste Ableitung = 0
f'(1) = 0
3*a*1² + b = 0
3a + b = 0 .................(1)
.
man kennt den Punkt (-1/+1)
f(-1) = +1
a*(-1)³ + b*(-1) = 1
-a - b = 1 .............(2)
.
(1) und (2) addieren, um b zu eleminieren
3a - a + b - b = 0 + 1
2a = 1
a = 0.5
einsetzen in (1) oder (2)...in(2)
-0.5 -b = 1
-0.5 - 1 = +b
-1.5 = b
.
f(x) = 0.5x³ - 1.5x
Das war die übliche Art, die man üblicherweise, bevor Integrale Stoff werden, lernt .
.
.
.
B)))))
Nullstellenform
Vorwort , Einleitung
Die Parabel x² -x - 12 hat die Nullstellen -3 und +4
x² -x - 12 = (x+3)(x-4)
letzteres nennt man Nullstellenform
Auch 4x² - 4x - 48 = 4*(x² -x - 12) hat die Nullstellen -3 und +4
.
Man kann die Parabelfkt auch so schreiben a*(x - NST1)(x - NST2)
.
Weil hier eine Fkt mit Grad 3 vorliegt , gilt hier
a*(x - NST1)(x - NST2)(x - NST3)
.
die 3 NST kennt man -w(3) , 0 und +w(3) , aber a noch nicht
a*(x - -w(3) )(x - 0)(x - +w(3) )
a*(x² - 3)*x
a*(x³-3x)
und a ? mit (-1/1) schreibt man
1 = a * ( (-1)³ - 3 * -1 )
1 = a*(-1 + 3)
1 = a*2
0.5 = a
.
Aus a*(x³-3x)
wird also
0.5(x³-3x) = 0.5x³ - 1.5x
bingo , so wie oben
Vielen Dank! Jetzt habe ich es dank Ihnen verstanden. :)
Was ist denn das Komplizierte? Das Aufstellen der Funktionsgleichung oder das Ausrechnen des Integrals?
Bzgl. der Funktionsgleichung kennst Du alle 3 Nullstellen, also nutzt Du die Nullstellenform f(x)=a*(x-x1)(x-x2)(x-x3) mit den Nullstellen bei x1, x2 und x3 und den Punkt (-1|1) oder (1|-1) um an den Streckungsfaktor a zu kommen. Eine dieser "Klammern" ist nur das x und die anderen beiden lassen sich mit der dritten binom. Formel zusammenfassen, somit sind auch die Wurzeln aus dem Term.
Hast Du die Funktionsgleichung brauchst Du "nur noch" von -Wurzel(3) bis 0 und von 0 bis 1 integrieren und die Beträge daraus addieren. Alternativ könntest Du von -1 bis 0 integrieren, das wegen der Symmetrie mit 2 multiplizieren plus dem Integral von -Wurzel(3) bis -1).
Hat eine Funktion z. B. die Nullstellen 1, 2 und 3, dann muss der Funktionsterm in der Linearfaktorzerlegung a*(x-1)(x-2)(x-3) lauten! Denn was sind ganz offensichtlich die Nullstellen dieses Terms...?
Also hast Du hier den Term a*(x-(-W(3))*(x-0)*(x-W(3))=ax(x+W(3))*(x-W(3))
Die beiden letzten Klammern ergeben (3. binom. Formel) (x²-3), also lautet die Funktionsgleichung bis hierhin: f(x)=ax(x²-3).
Jetzt den Punkt (1|-1) einsetzen, a ausrechnen, ausmultiplizieren, integrieren...
Für sowas gibt's normalerweise das Integral.
Einmal von - SQRT(3) bis 0 und einmal von 0 bis 1.
Das ist mir schon bewusst. Allerdings braucht man dafür erstmal eine Funktionsgleichung, und genau diese ist nicht gegeben.
Mit den Nullstellen und Extremwerten sollte sich das aber berechnen lassen.
Ich habe meine Frage in diese Plattform reingestellt, damit mir jemand den Rechenweg zeigt, damit ich es besser nachvollziehen kann.
Ich verstehe die Nullstellenform nicht.