Inhalt der Fläche berechnen (Integrale mit GTR)?
Hallo,
ich habe folgende Aufgabe mit den Lösungen jedoch weiß ich nicht wie mein Lehrer darauf kommt. Weiß irgendjemand was NST bedeutet und wie der Rechenweg lautet da ich bald eine wichtige Klausur schreibe.
Danke für eure Hilfe Bilder sind im Anhang


3 Antworten
NST dürften die Nullstellen sein, aber ich frage mich, wie dein Lehrer hier auf 0 und 4 kommt... Vermutlich ein Tippfehler (s. u.)
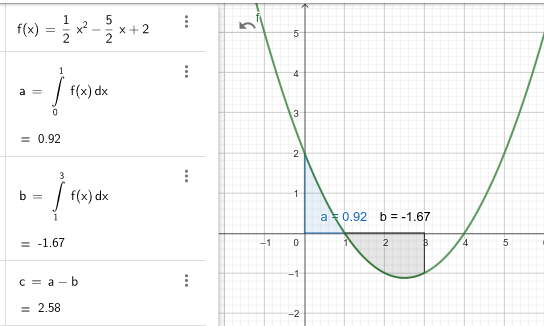
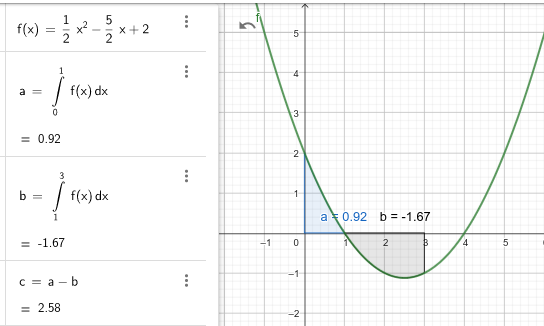
Prinzipiell hast du ja einen GTR zur Verfügung also wäre für mich der erste Schritt, mir den Graphen der Funktion einmal anzugucken. Da siehst du, dass deine Funktion die X-Achse an zwei Stellen schneidet. Kann dein Taschenrechner Nullstellen bestimmen? Wenn ja kommst du schnell auf die Nullstellen 1 und 4 (dass 0 keine Nullstelle ist, sieht man ja auch schon an dem +2 in der Formel).
Da die 4 außerhalb deines [0, 3] Intervalles liegt, musst du nur die erste Nullstelle, also die 1 berücksichtigen. Nun bildest du eine Stammfunktion zu f(x) (-> Integrieren).
In diese Stammfunktion würdest du jetzt die Grenzen deines Intervalles einsetzen, um den Flächeninhalt zu berechnen. Für die Stammfunktion F(x) fürdest du also rechnen F(3) - F(0).
Aber: Dieser Flächeninhalt ist gewichtet (!). Du würdest jetzt also den Teil unter der X-Achse von dem Teil über der X-Achse abziehen.
Da du das nicht willst, musst du einmal die Werte von 0 und 1 (der erste Abschnitt, vor der Nullstelle) und einmal die Werte von 1 und 3 (der zweite Abschnitt, ab der Nullstelle) einsetzen. Die Beträge der Ergebnisse addierst du dann. Insgesamt ergibt sich also
A = | F(1) - F(0) | + | F(3) - F(1) |
Macht das für dich Sinn? Ansonsten frag gerne nochmal genauer nach :)
Wenn man eine vom Graph und der x-Achse eingeschlossene Flächen berechnen muss, benötigt man Nullstellen (so verstehe ich auch "NST"), und man prüft, ob die Nullstellen im Intervall des zu berechnenden Integrals liegen. Allerdings ist die Prüfung hier bei Aufgabe a) falsch, denn die eine Nullstellen ist x=1 und nicht bei x=0. Daher muss man das Integral aufteilen in
(Im Bereich 1 bis 2 liegt der Graph der Funktion unterhalb der x-Achse und daher wäre das Integral negativ und daher muss für das Intervall [1;3] der Betrag des Integrals genommen werden).
Gerechnet wurde dann aber in der Lösung korrekt von 0 bis 1 und von 1 bis 3, sonst wäre das Ergebnis in der Lösung nicht ebenfalls ungefähr 2,58 wie unten.
NST bedeutet Nullstelle. Der Rechenweg lautet so dass du zunächst die Nullstellen der jeweiligen Funktion berechnest und dann von Nullstelle zu Nullstelle das bestimmte Integral berechnest. Ist das Ergebnis einer Teilrechnung negativ, drehst du das Vorzeichen um. Dann addierst du alle Teilergebnisse auf. Was genau das doppelte ~ da soll weiß ich auch nicht, man kann die Fläche exakt als Bruch angeben,
Das "Ungefähr" ist wohl wieder mal der Kniefall vor einer falsch verstandenen "Anschaulichkeit".