Flächenberechnung einer Polynomfunktion
High there!
Ich wollt nur kuzr meine Berechnung überprüfen lassen, ob das Ergebnis eh stimmt. ^^
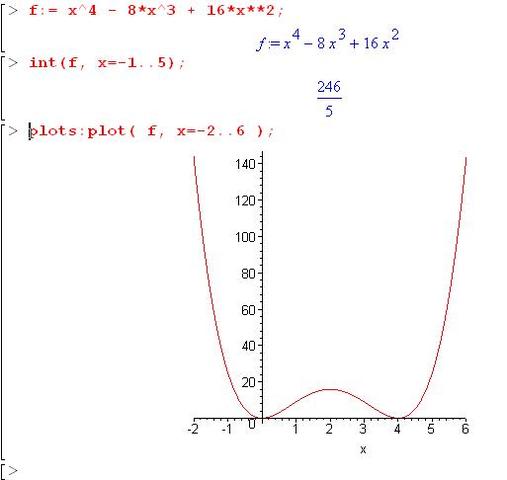
Ich habe die Funktion x^4 - 8x³ + 16x² und musste da die Fläche im intervall von [-1 / 5] berechnen.
Ich komme da auf 49,2 E². Stimmt das? Ich habe hier einfach die Funktion in den Taschenrechner eingegeben und danach das integral von ihm ausrechnen lassen.
Hoffe es macht sich wer die Mühe das nachzurechnen. ^^
p.s. die Funktion sieht wie ein W aus. Und da ich hier Nullstellen habe, welche auch gleichzeitig Extremwerte sind, so muss ich (denke ich) die Integralrechnung nicht aufsplitten. (Stimmt doch, oder?)
Schon mal danke vorweg, Leute! xD
3 Antworten
Ja, das hat Maple auch heraus.
Hallo !
f(x) = x ^ 4 - 8 * x ^ 3 + 16 * x ^ 2
F(x) = ∫ ( x ^ 4 - 8 * x ^ 3 + 16 * x ^ 2) * dx = (1 / 5) * x ^ 5 - 2 * x ^ 4 + (16 / 3) * x ^ 3 + C
Mit C = 0
F(5) = 125 / 3 = 625 / 15
F(-1) = -113 / 15
F(5) - F(-1) = 625 / 15 - (-113 / 15) = 738 / 15 = 49.2
LG Spielkamerad
sagt mein TR auch; da du das Rechnen eh dem TR überlässt, check nochmal, ob du dasselbe rausbekommst, wenn du von -1 bis 0 und von 0 bis 4 und von 4 bis 5 einzeln die Flächen berechnest und dann addierst.