Fakultät berechnen für n!=6
Hallo,
n!=6
ich wollte mal wissen ob es eine Möglichkeit gibt die Gleichung n!=6 nach n aufzulösen. In diesem Beispiel ist mir bewusst das n=3 ist aber mich interessiert ob es eine verallgemeinerung gibt.
Danke schonmal :)
5 Antworten
Das kannst du ganz genauso iterativ berechnen wie die Fakultät selber:
Sei die Gleichung n! = a gegeben.
Dann rechnest du
a * 1/2 * 1/3 * 1/4...
solange, bis es entweder nicht aufgeht (dann ist a keine Fakultät), oder bis 1 herauskommt. Der letzte Nenner ist dann das gesuchte n.
In deinem Beispiel:
6 * 1/2 * 1/3 = 1, also n=3.
Ganz genau. Der Trick ist eben, bei den kleinen Zahlen anzufangen - man weiß ja nicht, welches der letzte Faktor ist, aber die ersten kennt man ja.
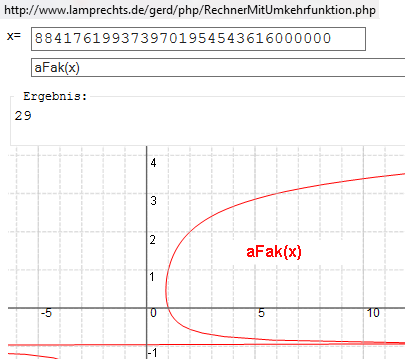
Auch das kann der Umkehrfunktionen Rechner:
http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
aFak(x) bis etwa 8841761993739701954543616000000
Aber wegen der Gammafunktion auch für reelle Zahlen:
aFak(-5)= -1.24332781666006550023998939322095...
denn Fak(x)=x! = Gamma(x+1)
Die Berechnungen sind sehr komplizierte Iterationen...
Kurz: Nein, da Fakultät keine injektive Funktion ist und demnach keine Umkehrfunktion hat. Man könnte ein Programm schreiben, das prüft, ob eine Zahl eine Fakultät einer anderen Zahl ist und dann den Wert oder keine Fakultät zurückgibt.
Siehe auch hier:
Ne, es gibt schließlich nur ganz wenige Zahlen, die die Fakultät von irgendwas sind.
Dafür müsstest du mit der Gammafunktion arbeiten und sie invertieren. Siehe den zugehörigen Wiki-Eintrag und diese Diskussion: http://www.matheplanet.com/matheplanet/nuke/html/viewtopic.php?topic=16556
Man könnte ja auch sagen, man dividiere die Zahlen, die definitionsgemäß die Fakultät bilden, sukzessive heraus (2, 3, 4 usw.)