e^x -x muss doch einen Wendepunkt haben oder?
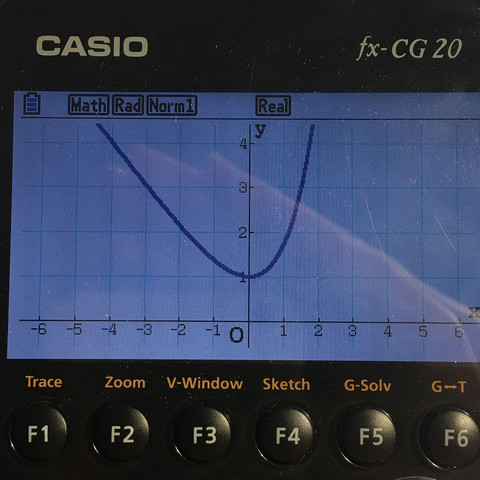
Hallo, auf dem Bild seht ihr die Funktion e^x -x, die eigentlich doch einen Wendepunkt haben muss. Aber weil f‘‘(x) keine Nullstelle hat, kann ich das nicht ausrechnen. Kann mir bitte jemand helfen? Danke!
8 Antworten
Also ich sehe keinen Wendepunkt. Die Funktion ist in dem Ausschnitt, den wir sehen, linksgekrümmt. :)
siehe Mathe-Formelbuch,"Kurvendiskussion"
Bedingung "Maximum" f´(x)=0 und f´´(x)<0
" "Minimum" f´(x)=0 und f´´(x)>0
" "Wendepunkt" f´´(x)=0 und f´´´(x) ungleich Null
" "Sattelpunkt" f´´(x)=0 und f´´´(x) ungleich Null und f(xw)=0
Hinweis: Der "Sattelpunkt" (nennt man auch Terrassenpunkt) ist ein spezieller Wendepunkt,bei dem die Steicgung f´(x)=m=0 ist.
Die Tangente liegt hier "parallel" zur x-Achse.
also f(x)=e^x-x abgeleitet
f´(x)=e^x-1 noch mal abgeleitet
f´´(x)=e^x hier kann e^x nicht zu Null werden!!
also kein "Wendepunkt"
mit x=0 ergibt e^0=1
mit x<0 ergibt e^-x wird unendlich klein,aber nicht Null (außer man betrachtet den lim)
mit x>0 wird e^x unendlich groß
Hallo,
wie die anderen bereits schrieben und wie Du es auch an der Graphik und natürlich an der zweiten Ableitung erkennen solltest, hat die Funktion keinen Wendepunkt.
Wieso auch? Das Ding kommt aus dem Unendlichen, hat ein Minimum und verschwindet wieder ins Unendliche.
Kein Grund, das Steuer von links nach rechts zu drehen.
Du befindest Dich die ganze Zeit in einer Linkskurve, die beim Minimum am steilsten wird und dann immer flacher bis in alle Ewigkeit, ohne daß es irgendwann mal geradeaus geht oder gar in eine Rechtskurve mündet.
Herzliche Grüße,
Willy
Eines der üblichen Missverständnisse?
Ein Wendepunkt ist NICHT ein Punkt, in dem es vom Fallen ins Steigen übergeht oder umgekehrt (das ist ein relativer Tiefpunkt/Hochpunkt), sondern ein Punkt, in dem der Graph von einer Rechtskurve in eine Linkskurve übergeht oder umgekehrt.
Ist die Ableitung von e^x - x nicht e^x - 1? Die Ableitung hat schon eine Nullstelle. Edit: Meinst du die erste oder die zweite Ableitung?
Ich dachte, wenn die erste Ableitung 0 ergibt, dann ist an der Stelle ein Wendepunkt.
Aber für den Wendepunkt braucht man die 2. und 3. Ableitung und die sind beide e^x