Beweis dafür, dass das Quadrat einer geraden Zahl, eine gerade Zahl ist?

Mein Prof hat heute so bewiesen, dass das Quadrat einer geraden Zahl eine gerade Zahl ist.
Mal ganz davon abgesehen, dass offensichtlich das Quadrat einer geraden Zahl eine gerade Zahl ist, finde ich den Beweis schwierig.
Erst wird die Zahl x als gerade definiert. Dann wird die Gleichung quadriert und es wird überprüft, ob die Bedingung, die x als gerade definiert immer noch erfüllt wird.
Bei dieser Überprüfung wird folgendermaßen vorgegangen: 2n ist die Definition von gerade. Die Definition von gerade zum Quadrat ist ebenfalls gerade. Das doppelte der Definition von gerade zum Quadrat ist ebenfalls gerade. Damit ist das Quadrat einer geraden Zahl gerade.
Aber wir wollen doch beweisen, dass eine Zahl zum Quadrat gerade ist. Da kann doch nicht der kern der Begründung sein, dass die Definition von gerade zum Quadrat ebenfalls gerade ist. Das ist als würde ich Beweisen, dass ein Baum ein Baum ist, weil er ein Baum ist.
2 Antworten
von x = 2n bis zu x² = 4n² werden erlaubte Umformungen angewandt.
.
und hier
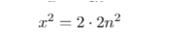
ist nur die 2 vorne entscheidend, denn alles mal 2 ist eben gerade.
.
alles gut finde ich
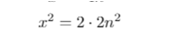
ah ja die zwei vorne ist entscheidend lol ich sollte mal ne pause machen
Ein mathematischer Beweis hat drei Teile: Voraussetzung, Behauptung und Begründung. In der Begründung muß aus der Voraussetzung die Behauptung gefolgert werden. Der Prof. hat wohl bewußt einen extrem einfachen Beweis gewählt um das Prinzip eines Beweises herauszuarbeiten.
Vor: x = 2 * n ; wobei n ganze Zahl sein soll ;
Beh.: (x^2) = 2 * N ; wobei N ganze Zahl sein soll ;
Begr.: x = 2 * n , => x^2 = (2 * n)^2 = 4 * n^2 = 2 * 2 * n^2 = 2 * N mit N = 2*n^2.