Anwendungsaufgabe Integrale?

Guten Tag,

bei dieser Aufgabe komme ich im Gegensatz zu den Lösungen bei der zweiten Ableitung auf +0.12. eigentlich ist ja auch wenn die zweite Ableitung positiv und nicht negativ ein Tiefpunkt…

aber wie ist das, wenn die zweite Ableitung überall gleich ist, hat sie dann überhaupt noch eine Aussagekraft?

lg

Answer 1

[evtldocha]

aber wie ist das, wenn die zweite Ableitung überall gleich ist, hat sie dann überhaupt noch eine Aussagekraft?

Ja, das hat eine Aussagekraft und das ist bei jeder quadratischen Funktion so, die bekanntlich nur einen einzigen Extremwert haben kann - entweder ein Minimum oder ein Maximum.

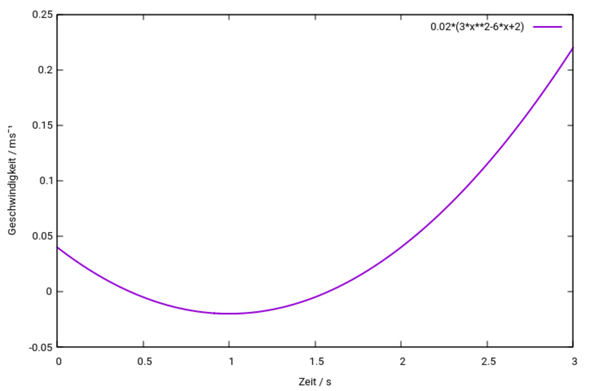
Die Lösung im Bild zu 4a) ist natürlich Quark, weil nur aus v''(t) > 0 das Minimum für v(t) folgt.

Answer 2

[indiachinacook]

Du siehst, daß die Geschwindigkeit bei t=1 s minimal ist. Das kann man natürlich auch einfach berechnen:

v(t) = 1⁄50 ⋅ (3x²−6x+2)
v’(t) = 1⁄50 ⋅ (6x−6) = 3⁄25 ⋅ (x−1)
v’’(t) = 3⁄25

Um das Minimum zu finden, setzt Du die erste Ableitung Null und bekommst x−1=0 bzw. x=1. Die zweite Ableitung ist positiv, also handelt es sich wirklich um ein Mini­mum (daß v’’ konstant ist, hat dabei keine Bedeutung, weil wir uns ja nur für v’’(1) interessieren).

Answer 3

[Halbrecht]

wenn die zweite Ableitung einfach nur eine Zahl Z ist ,dann gilt eben ohne weitere Rechnung

Z > 0 , dann TP
Z < 0 , dann HP

easy as possible :))