Analysis Lückentext?
hallo, kann mir jemand diesen Lückentext anhand der Funktion ausfüllen und die Lösungen der jeweiligen Lücken erklären?


Was würdest du denn rein schreiben?
Ich hätte keine Ahnung weil unser Mathelehrer nichts erklären kann
2 Antworten
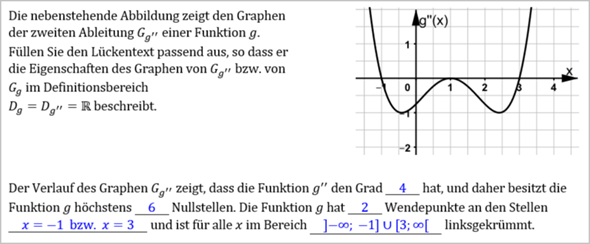
Bemerkung: Da in der Abbildung der Graph von g′′ nur für x im Bereich zwischen etwa -1,5 und etwa 3,5 zu sehen ist, kann man eigentlich nicht auf den gesamten Verlauf schließen. Der Grad der Funktion g könnte daher beispielsweise auch größer als 6 sein; es könnte weitere Wendepunkte geben; der Bereich, in dem der Graph von g linksgekrümmt ist, könnte kleiner sein.
Ansonsten:
- Der Verlauf des Graphen von g′′ mit dieser W-Form sieht typisch für den Graphen einer Funktion 4-ten Grades aus. Dementsprechend hat dann g den Grad 6 (da 2 höher als der Grad der zweiten Ableitung).
- Eine ganzrationale Funktion g hat höchstens so viele Nullstellen, wie ihr Grad ist; hier also höchstens 6.
- Die Funktion g hat dort Wendepunkte, wo die Funktion g′′ ihr Vorzeichen wechselt. Dies ist hier an den beiden Stellen x = -1 bzw. x = 3 der Fall
- Der Graph der Funktion g ist dort linksgekrümmt, wo g′′ positiv ist. (Bzw. zählen auch isolierte Nullstellen von g'' am Übergangsbereich noch dazu.) Dies ist hier für x ≤ -1 sowie für x ≥ 3 der Fall.
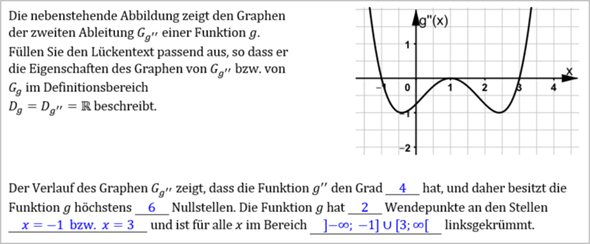
das geübte Auge erkennt Grad 4 . Die Struktur passt aber auch zu Grad u.a .
Vermutlich hat Mihisu das selbst fabriziert : er sie kann das . Die Verwendung von eckigen Klammern statt ( deutet auch darauf hin
Ein bisschen seltsam die Notation bei euch an der Schule.
Aber die Antwort sollte lauten:
Der Verlauf des Graphen g'' zeigt, dass die Funktion g'' den Grad 3 hat und daher besitzt die Funktion g höchstens 5 Nullstellen. Die Funktion hat Wendepunkte an den Stellen -1 und 3 und ist für alle x im Bereich [-1 ; 3] linksgekrümmt.
Was du machst, ist eine Kurvendiskussion. Wichtig sind dabei Hoch- & Tiefpunkte sowie Wendepunkte, die man betrachtet.
g''(x) ist die zweite Ableitung von g. Zählst du die Nullstellen von g'', so kommst du auf 3. g''(x) ist also ein Polynom 3. Grades
g''(x) = ax^3 + bx^2 + cx + d
Also muss g(x) mit zwei Strichelchen weniger ein Polynom 5. Grades sein und hat somit höchstens 5 reelle Nullstellen.
Dort, wo bei g''(x) die Nullstellen sind, hat g(x) Wendepunkte, wenn g'''(x) also die dritte Ableitung ungleich 0 ist. Folglich darf der Anstieg von g''(x) an den Stellen nicht 0 sein. Dies ist bei -1 und 3 der Fall.
Solange g''(x) negativ ist, ist g (x) nach links gekrümmt. Das ist der Fall im Intervall [-1 ; 3] zwischen beiden Wendepunkten.
Die Stelle 1 ist übrigens furchtbar kompliziert. Das könnte ein Sattelpunkt sein, aber den Beweis dafür führt man erst im Studium.
Ich hoffe, ich habe keine Fehler gemacht.
Zusätzlich zu den vorigen Kommentaren zum Grad...
Solange g''(x) negativ ist, ist g (x) nach links gekrümmt.
Nein. Dort wo g′′ negativ ist, ist g rechtsgekrümmt. Dort wo g′′ positiv ist, ist g linksgekrümmt.
g'' hat doch offensichtlich einen geraden Grad. Dieser beträgt 4. Dementsprechend hat g Grad 6 und damit höchstens 6 NST.
Du hast recht, dass in dem Satz vom Grad g'', statt vom Grad von g, die Rede ist.
Trotzdem ändert das nichts daran, dass das, was petronex geschrieben hat, korrekt ist; und dass die Antwort mit dem Grad 3 für g′′ und dem Grad 5 für g leider falsch ist.
Der Verlauf des Graphen g'' zeigt, dass die Funktion g'' den Grad 3
Das "W" ist der typische Verlauf eines Polynoms 4. Grades (Achsensymmetrie - schon deswegen muss es ein gerades Polynom sein) und das hat Konsequenzen für die maximale Zahl der Nullstellen von g.
Vielen Dank! Darf ich fragen woher sie diesen Ausschnitt der Übung her haben? Ist die aus irgendeinem Übungsheft oder sowas?