Analysis Hilfe?
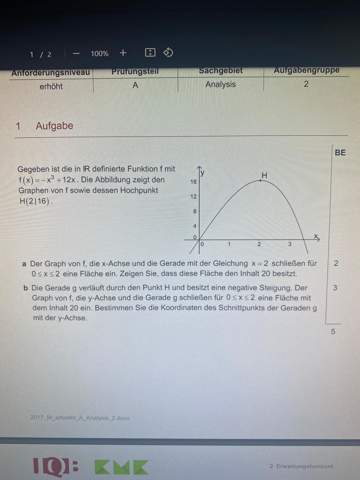
Kann mir jemand bei der Aufgabe b helfen?Verstehe die Lösung überhaupt nicht.Was sollte man da machen?
1 Antwort
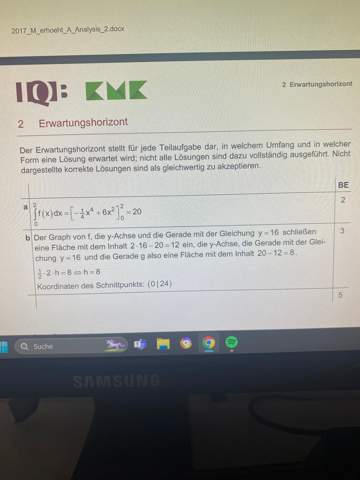
Zu b): Der Punkt H = (2,16) ist bekannt. Die Gerade g soll durch diesen Punkt verlaufen und sie soll eine negative Steigung besitzen. Sie sollen die Koordinaten des Schnittpunktes der Gerade g mit der y-Achse bestimmen. Dafür müssen Sie die Funktionsgleichung der Gerade kennen. Allerdings gibt es unendlich viele Geraden, mit einer negativen Steigung, die den Punkt H berühren.
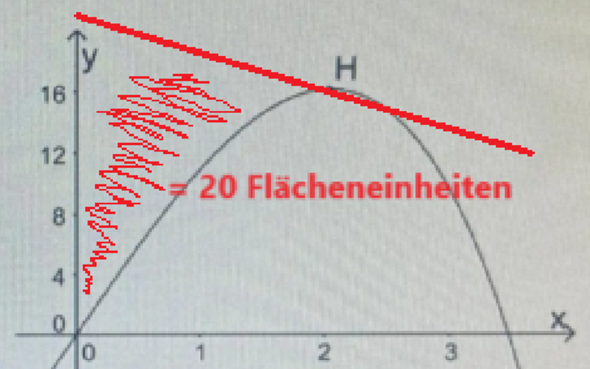
Die Information "Der Graph von f, die y-Achse und die Gerade g schließen für 0 =< x =< 2 eine Fläche mit dem Inhalt 20 ein." muss also der Schlüssel zur Lösung der Aufgabe sein. Welche Fläche damit gemeint ist, ist hier einmal skizziert:
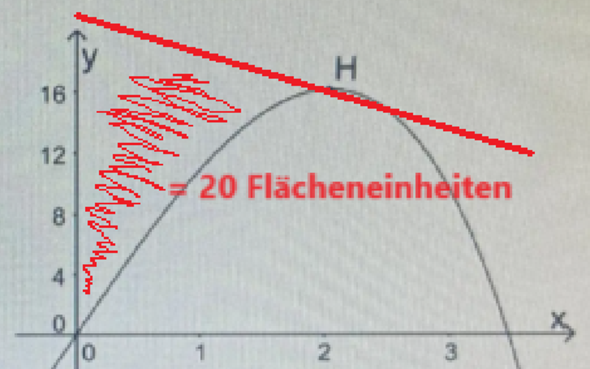
Mathematisch bedeutet das, dass das Integral der Funktion g von 0 bis 2 abzüglich des Integrals der Funktion f von 0 bis 2 gleich 20 ist:
Für g, deren Funktionsgleichung noch nicht bekannt ist, wird einfach die allgemeine Form ax+b eingesetzt. Im Anschluss müssen die Terme integriert werden und die Integrationsgrenzen eingesetzt werden. Auch allgemeine Ausdrücke wie ax+b lassen sich integrieren. Für das Integrieren und das Einsetzen der Grenzen verwende ich den Integralrechner (Link). Selbstverständlich lässt sich dies mit den gewohnten Rechenregeln auch händisch erledigen.
Zudem wissen Sie, dass g durch h verläuft. Es muss also gelten:
Beide Gleichungen bilden ein lineares Gleichungssystem und dieses lässt sich lösen um a und b zu ermitteln.
b bestimmen:
a bestimmen:
a und b sind bekannt, also lautet die vollständige Funktionsgleichung für g:
Der Schnittpunkt der Gerade g mit der y-Achse liegt bei x = 0 und die y-Koordinate ist dann eben gleich dem y-Achsenabschnitt aus der Funktionsgleichung, also liegt der Schnittpunkt bei (0,24).