Analysis alte Abiprüfung?

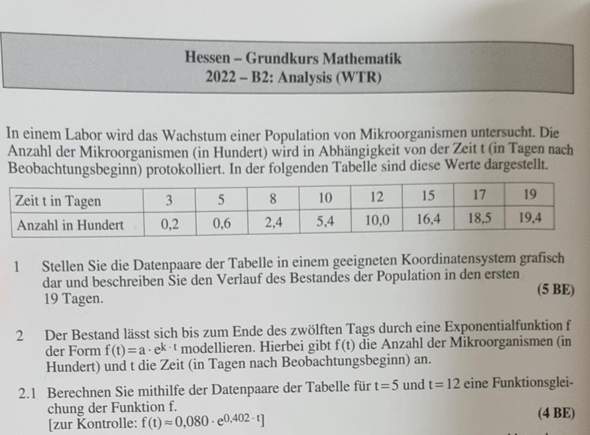
Wie kommt man bei 2.1 auf die Funktion genau? Also was rechnet man?

Answer 1

[mihisu]

Du sollst die Datenpaare bei t = 5 und t = 12 verwenden. Die entsprechenden Funktionswerte kannst du der Tabelle entnehmen. Bei t = 5 kann man in der Tabelle f(t) = 0,6 ablesen. Und bei t = 12 kann man in der Tabelle f(t) = 10,0 ablesen.

Setzt man diese beiden Datenpaare in den Ansatz f(t) = a ⋅ e^(k ⋅ t) ein, erhält man die beiden Gleichungen...

$[\text{G}1]:\quad a\cdot e^{k\cdot 5}=0\text{,}6$

$[\text{G}2]:\quad a\cdot e^{k\cdot 12}=10\text{,}0$

Diese bilden ein Gleichungssystem mit zwei Gleichungen und den beiden Unbekannten a und k, was man lösen kann.

Man kann nun beispielsweise [G2] durch [G1] dividieren, damit sich a rauskürzt und man eine Gleichung erhält, die nur noch eine einzige Unbekannte (nämlich k) enthält.

$\frac{a\cdot e^{k\cdot 12}}{a\cdot e^{k\cdot 5}}=\frac{10\text{,}0}{0\text{,}6}$

$\Leftrightarrow\quad \frac{e^{k\cdot 12}}{e^{k\cdot 5}}=\frac{10\text{,}0}{0\text{,}6}$

$\Leftrightarrow\quad e^{k\cdot 12-k\cdot 5}=\frac{10\text{,}0}{0\text{,}6}$

$\Leftrightarrow\quad e^{k\cdot \left(12-5\right)}=\frac{10\text{,}0}{0\text{,}6}$

$\Leftrightarrow\quad e^{k\cdot 7}=\frac{10\text{,}0}{0\text{,}6}$

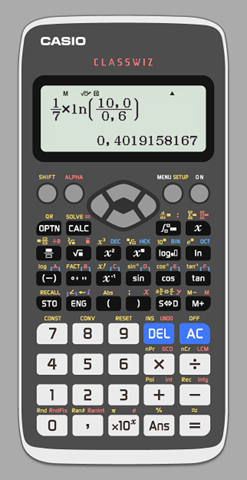
[Anwenden des natürlichen Logarithmus.]

$\Leftrightarrow\quad k\cdot 7=\ln\left(\frac{10\text{,}0}{0\text{,}6}\right)$

$\Leftrightarrow\quad k=\frac{1}{7}\cdot \ln\left(\frac{10\text{,}0}{0\text{,}6}\right)$

$k\approx 0\text{,}402$

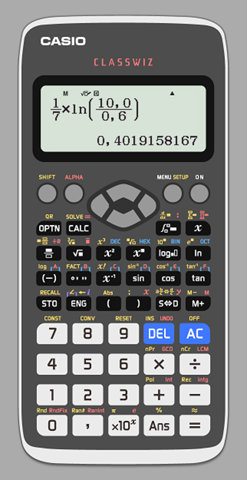
Diesen Wert für k kann man nun in eine der beiden Gleichungen [G1] oder [G2] einsetzen, und damit dann den Wert a berechnen. Beispielsweise unter Verwendung von [G1]...

$a\cdot e^{k\cdot 5}=0\text{,}6\quad \rightarrow\quad a=\frac{0\text{,}6}{e^{k\cdot 5}}\approx \frac{0\text{,}6}{e^{0\text{,}402\cdot 5}}\approx 0\text{,}080$

Setzt man nun die beiden berechneten Werte a ≈ 0,080 und k ≈ 0,402 in den Ansatz f(t) = a ⋅ e^(k ⋅ t) ein, erhält man die gesuchte Funktionsgleichung...

$\boxed{f(t)\approx 0\text{,}080\cdot e^{0\text{,}402\cdot t}}$

Answer 2

[FataMorgana2010]

Du hast eine Funktion der Form

$f(t) = a \cdot e^{k \cdot t}$ Die hat zwei unbekannte Parameter, nämlich a und t. Dazu brauchst du jetzt zwei Gleichungen, um diese Parameter auszurechnen. Du sollte die Paare (5;0,6) und (12;10,0) nehmen. Das setzt du ein

f(5) = 0,6

f(12) = 10

Also:

$a \cdot e^{k \cdot 5} = 0,6$ und

$a \cdot e^{k \cdot 12} = 10$ Aus diesen beiden Gleichungen kannst du jetzt die Parameter berechnen.

Da in beiden Gleichungen der Faktor a vorkommt, bietet es sich an, die beiden Gleichungen durcheinander zu teilen (das geht, weil nirgendwo Null rauskommen kann):

$\frac{a \cdot e^{k \cdot 5}}{a \cdot e^{k \cdot 10} } = \frac{0,6}{10}$ Das a kürzt sich weg und mittels der Potenzgesetze und dem Logarithmus kannst du schnell k ausrechnen. Das setzt du dann in eine der beiden Gleichungen von oben ein und schon hast du auch a.

Answer 3

[Vampirjaeger]

Du hast den Funktionterm den Form f(t)=a*e^(kt) vorgegeben. Setzen die beiden Zahlenpaare (5; 0,6) und (12; 10,0) ein und lösen das entstehende Gleichungssystem, um a und k zu berechnen.