Wo liegt der Unterschied von einer Geometrische Reihe zu einer Harmonischen Reihe?
2 Antworten
Die Geometrische Reihe
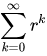
konvergiert für alle |r| <1 gegen den Grenzwert 1/(1-r)
Ein prominentes anekdotisches Beispiel dieser Reihe kennen wir aus der Geschichte von Achill und der Schildkröte. Oder den Kuchenesser, der immer die Hälfte seines Kuchens isst und deswegen den Kuchen nie ganz aufisst, auch wenn die Größe der Stücke sich bei jedem Vorgang halbiert.
Die Harmonische Reihe, auch Zeta(1),
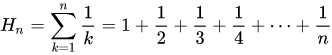
konvergiert nicht, sondern wächst erstaunlicherweise logarithmisch mit der Anzahl der Reihenglieder.
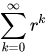
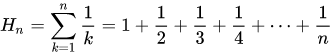
Naja,
harmonische Reihe ist divergent und Summe aller Kehrbrüche von natürlichen Zahlen
Bei der geo. Reihe fehlen viele Glieder, die die harmonische Reihe hat, stattdessen ist sie in der Form q^k vorzufinden. Sie ist für |q| < 1 konvergent