Geometrische Reihe: Differenz zum Grenzwert bestimmbar?
Hi,
Nehmen wir an, ich habe eine geometrische Reihe, zB
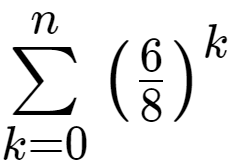
Für n ins unendliche hat dieser Term den Grenzwert 4.
Gibt es dann irgendeine Möglichkeit, für ein beliebiges n die Differenz des obigen Terms zu diesem Grenzwert zu bestimmen?
zum Beispiel wäre das für n = 1 noch 2,25, für n = 10 aber schon ca. 0,1689.
Das würde mir bei einem Beweis sehr weiterhelfen.
Danke im Voraus!
Also scheinbar scheint diese Differenz immer durch 3 * (6/8)^n gegeben zu sein. Aber warum?
Ich habe jetzt nach einigem Ausprobieren folgendes herausgefunden:Die Differenz zum Grenzwert ist für ein n für jede geometrische Reihe mit Bruch z gegeben durch
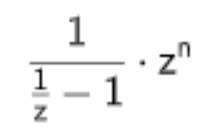
Hat irgendwer von euch eine Ahnung, warum das so ist?
1 Antwort
Hallo,
einfach die Summenformel für geometrische Reihen benutzen:
q^0+q^1+q^2+...+q^n=(1-q^(n+1))/(1-q).
q wäre in Deinem Fall 6/8=3/4.
Gewünschtes n einsetzen und den Term von 4 abziehen.
Für n=10 wäre das 4-(1-(3/4)^11)/(1/4)=0,16894 (gerundet).
Herzliche Grüße,
Willy
Wenn Du bedenkst, daß der Grenzwert für n gegen unendlich einer geometrischen Reihe bei 1/(1-q) liegt, kannst Du 1/(1-q)-(1-q^(n+1))/(1-q) leicht zu Deiner Formel umformen. Versuch's mal, ist eine gute Übung. Meinem q entspricht dabei Dein z.