wo ist der Hoch und Tiefpunkt? Thema : quadratische Funktionen?
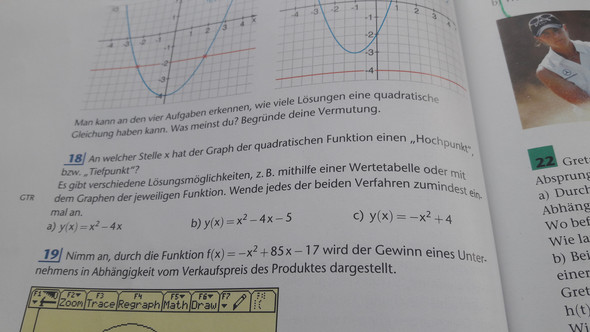
Ich brauche Hilfe bei Aufgabe 18 . Diese lautet : An welcher Stelle x hat der quadratische Graph der quadratischen Funktion einen 'Höhepunkt bzw. Tiefpunkt ? Meine Frage ist wo befindet sich der Hoch und Tiefpunkt ? Also ich habe einen Graohen liegt der Punkt dann auf dem Graohen oder kann es auch der höchste Punkt sein der aber nicht die x oder y Achse schneidet
4 Antworten
zu 18c)
Wertetabelle
P1 (-2│0)
P2 (-1│3)
P3 (0│4)
P4 (1│3)
P5 (2│0)
Punkte in Koordinatensystem eintragen und Parabel einzeichnen.
allg. Form
y(x) = a * x² + b * x + c
y(x) = -x² + 4
Scheitelform
y(x) = a * (x – d)² + e
y(x) = (-1) * (x – 0)² + 4 = (-1) * x² + 4
Da a negativ ist, ist die Parabel nach unten offen. Der Scheitelpunkt S (0│4) ist in der Grafik und in der Scheitelform ablesbar. Er gibt, wegen a negativ, das Maximum der Funktion an.
Um Extremwerte zu berechnen kannst du die Erste und Zweite Ableitung nutzen, wenn du nachschauen möchtest, ob du mit deinem Ergebnis richtig liegst kannst du einen Grafikfähigen Taschenrechner benutzen oder das ganze Online über https://www.geogebra.org/ eingeben.
Die erste Ableitung musst du gleich 0 setzen
dann überprüfst du den aus der ersten Ableitung herausgefundenen Wert mit der zweiten Ableitung der Funktion.
Wenn das Ergebnis der zweiten Ableitung unter Null ist, handelt es sich um ein Maximum
Befindet sich der Wert über Null handelt es sich um ein Minimum.
Es gilt zu unterscheiden zwischen:
Lokales und globale Minimum sowie Lokales und globales Minimum.
Was meine ich damit?
Du kannst dir ja bei einem solchen Graphen immer einen bestimmten Bereich angucken, wenn du in diesem Bereich ein Minimum oder ein Maximum findest, muss das nicht zwingend das globale Minimum oder Maximum sein, da du du ja deinen Definitionsbereich verändert hast. Schaust du dir die gesamte Grafik an, so findest du dort vielleicht andere Werte, der Wert der am niedrigsten ist, wäre dann das globale Minimum und der Wert der am höchsten liegt wäre dann das globale Maximum.
Alles auch nochmal schön nachzulesen bei: https://www.mathebibel.de/extremwerte-berechnen
Erstmal danke für diese Ausführliche Antwort (die Inhaltlich auch Top ist), aber in der Aufgabenstellung wird nach Wertetabelle und vom Graphen ablesen gefragt.
Ableitungen wurden hier noch nicht geschult scheint es mir und helfen demnach hier auch nicht weiter.
Ok da du noch keine Ableitungen hattest würde ich dir eine Wertetabelle empfehlen:
lege eine Tabelle an mit x und f(x). Dann schreibe bei x so Werte von -4 bis 4 auf also
-4 -3 -2 -1 0 1 2 3 4
Diese Setzt du dann in die Funktion ein. Das sind deine dazugehörigen f(x) Werte
Dann Schaust du ob du eine Symetrie findest also ob du irgendwo einen Spiegel ansetzen kannst und auf beiden Seiten einer Zahl das selbe steht, denn quadratische Funktionen sind immer Symetrisch. Findest du zum Beispiel heraus, dass bei x=1 und x=3 Das selbe rauskommt und bei x=0 und x=4 das selbe rauskommt, so ist es wahrscheinlich, dass x=2 eine Extremstelle ist. Schaue dann einfach ob der f(x) wert bei x=2 größer ist als bei x=1 zum Beispiel (Dann ist dort ein Hochpunkt) oder kleiner (Tiefpunkt).
Am besten zeichnest du die Punkte aus der Wertetabbelle noch mal auf und dann siehst du auch den Tief- oder HochPunkt im Graphen
Das ist alles andere als eine Akademisch Wertvolle Lösung und später lernst du bessere Methoden (über 1. und 2. Ableitung ) aber im Moment reicht das aus.
Wenn du es nicht verstehst frag noch mal nach, ich weiß das war jetzt nicht optimal beschrieben.
nimm die Hälfte von der Zahl vor dem x und dreh das Vorzeichen um; wenn kein x da ist, dann x=0
also
a) x=2 Tiefpunkt
b) x=2 Tiefpunkt
c) x=0 Hochpunkt, weil Parabel nach unten geöffnet ist.
und danach kannst du ja ne Wertetabelle machen und für x zB -2,-1,0,1,2,3 einsetzen und wirst sehen, welcher y-Wert dann am größten bzw am kleinsten ist.