Wieso müssen Zeitdilatation und Längenkontraktion immer paarweise auftreten?

Hallo Lukas947,

"Zeitdilatation" und "Längenkontraktion" sind zwei Seiten derselben Medaille. Ich werde dies an einem Beispiel darlegen.

Wenn ein Raumfahrzeug B' an zwei als stationär betrachten Raumfahrzeugen A bei x = −d und B bei x = 0 vorbeizieht, mit konstanter Geschwindigkeit, die in einem von B aus definierten Koordinatensystem Σ als (v | 0 | 0), kann man auch B' als stationär ansehen; in einem von B' aus definierten Koordinatensystem Σ' sind es A und B, die sich mit (−v | 0 | 0) bewegen.

Beide Koordinatensysteme sind physikalisch gleichwertig, die Naturgesetze (= grundlegenden Beziehungen zwischen physikalischen Größen).

Die Strecke in Σ ist d, sodas B' die Zeit d/v braucht, um von A nach B' zu gelangen.

Zu den Naturgesetzen gehören auch MAXWELLs Grundgleichungen der Elektrodynamik und damit die elektromagnetische Wellengleichung mit der Naturkonstanten c. Daraus ergibt sich: Was sich relativ zu A und B mit c (bzw. 1 in Natürlichen Einheiten) bewegt, das bewegt sich auch relativ zu B' mit c bzw. 1 und umgekehrt.

Dies ist sie die Grundlage der Speziellen Relativitätstheorie (SRT), welche die "Zeitdilatation" und "Längenkontraktion" voraussagt. Sie greifen ineinander:

In Σ betrachtet ist der Zeittakt von B' um den Faktor

(1) γ := 1/√{1 − v²}

länger. Dadurch misst ein Beobachter um den Faktor 1/γ weniger Zeit.

In Σ' betrachtet ist der Abstand zwischen A und B nur d'=d/γ. Dementsprechend braucht B dann, wenn A gerade B' passiert, nur noch d/γv.

Tatsächlich sind die Wörter "Zeitdilatation" und "Längenkontraktion" irreführend. Sie suggerieren ein wüstes Gezerre und Gequetsche, wo in Wahrheit nur eine völlig gewaltfreie Projektionen vorliegt.

Und zwar entlang von Linien konstanter Zeit, die in Σ und Σ' unterschiedlich sind.

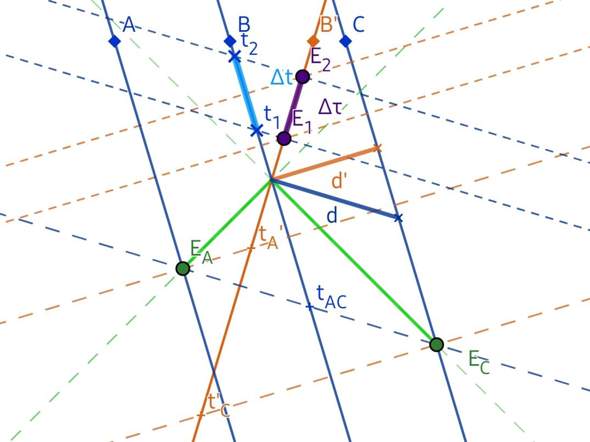
Bei x = d befinde sich ein drittes Raumfahrzeug C. Alle Fahrzeuge stehen in Funkkontakt; uns interessieren zwei Signale von A und C, die B und B' in dem Moment erreichen, wo sie aneinander vorbeiziehen.

In Σ müssen sie gleichzeitig abgeschickt worden sein, denn A und C sind gleich weit vom B entfernt.

In Σ' muss C sein Signal um den Faktor (1 + v)/(1 − v) =: K² früher abgesetzt haben als A, denn C war weiter und A weniger weit entfernt als zu dem Zeitpunkt, zu dem die Signale bei B und B' ankommen.

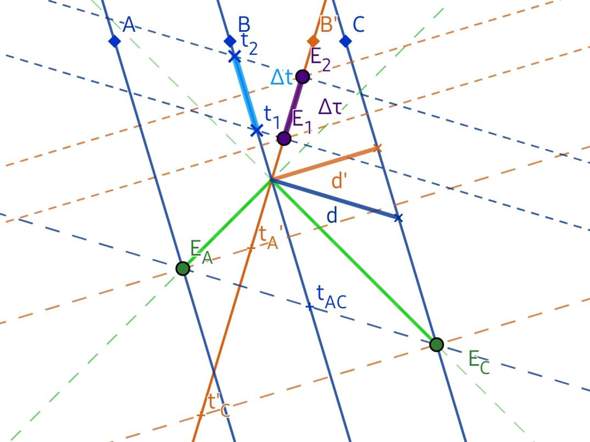
Abb. 1: Die Relativität der Gleichzeitigkeit zweier räumlich getrennter Ereignisse mit ihren Nebeneffekten.

__________________

¹) Eine derartige Konstante bietet einen natürlichen Weg, Strecken und Zeitspannen mit gleichen Maßstäben anzugeben, wodurch c=1 wird.

In der Astronomie tut man das tatsächlich: Man spricht von "Lichtsekunden", "Lichtminuten" etc. und "Lichtjahren". Im Alltag könnte man Nanosekunden (1ns≈30cm) und Mikrosekunden (1μs≈300m) verwenden. Geschwindigkeiten werden zu bloßen Zahlen, die man auch in ppb (parts per billion, Milliardstel) angeben kann.

Weil es eigentlich Ein und das Gleiche ist. Beides sind Hilfskonstrukte, damit man relativistische Effekte mit den Gleichungen der klassischen Physik greifen und berechnen kann.

Weil du sonst u.U. auf Überlichtgeschwindigkeit kommen könntest.

Nehmen wir an, Du fliegst eine Strecke von einem Lichtjahr mit hoher Geschwindigkeit, sodass der Lorentzfaktor sehr groß ist. Dann kannst Du diese Strecke in einer Bordzeit zurück legen, die kürzer ist als ein Jahr. Wenn sich für Dich nicht auch die Strecke entsprechend verkürzt hätte, kämst Du für Dich gerechnet auf Überlichtgeschwindigkeit. Das würde bedeuten, dass für "Dein"(sich bewegendes) Raketen-Bezugssystem andere physikalische Gesetze gelten und das widerspräche dem Einsteinschen Axiom, dass die Gesetze in allen Bezugssystemen gleich sind.

in einem Raum-Zeit-Kontinuum ist beides nicht voneinander zu trennen. Die Lichtgeschwindigkeit ist die Verbindung.