Zeitdilatation - Berechnung?
Kann mir jemand sagen, welche Werte ich wo in die Formel einfühen soll, damit ich das Beispiel korrekt berechnen kann?
Danke!
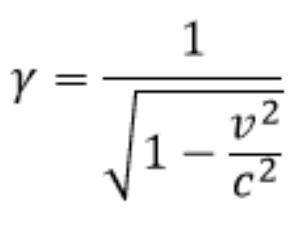

1 Antwort
Hallo Philipp171dwq,
so schwer ist das nicht. Es wird angenommen, dass die Enterprise mit konstantem Tempo (engl. speed) geflogen ist; zumindest soll es hier so gerechnet werden.¹)
Eine erdgebundenene Uhr nennen wir U wie "Uhr", die Borduhr der Enterprise nennen wir Ώ (gr. Ώρα ((h)ora), "Stunde").
Die von Ώ gemessene Zeitspanne Δτ für jeden Vorgang an Bord der Enterprise ist die Eigenzeit.
Von U aus gibt es keine direkte Messung, sondern aus Messwerten – unter Berücksichtigung der variierenden Entfernung und der Maßgabe, dass U stationär ist – wird eine Zeitspanne Δt berechnet. Wir nennen sie U- oder Σ- Koordinatenzeit. Wie der Name sagt, ist sie eine Koordinatendifferenz.
Relativitätstheorie ist Geometrie, und zwar raumzeitliche, und Σ ist ein von U aus definiertes Koordinatensystem mit der Weltlinie von U als Zeitachse.
Δt ist also eine Projektion des Vorgangs auf die Weltlinie von U, nicht der Vorgang selbst. Diese Sichtweise ist besser verständlich als das Wort "Zeitdilatation", das suggeriert, der Vorgang als solcher sei auseinandergezogen worden.
Der Vorgang kann darin bestehen, dass jemand im Bordbistro der Enterprise einen Cappuccino trinkt, aber auch die gesamte Reise sein, falls |v| konstant ist.
a) Δt = 5 JahreIst Δs = v∙Δt der zurückgelegte Weg, so ist die Eigenzeit durch
(1) Δτ = √{Δt² − Δs²⁄c²} = Δt∙√{1 − v²⁄c²}
gegeben. Da v = 0,84∙c ist, ergibt sich v²⁄c² = 0,7056, also ist der Ausdruck unter der Wurzel (bzw. innerhalb der "{}") 0,2944, und die Wurzel liegt bei ca. 0,5426. Das mal Δt ergibt etwa 2,7 Jahre.
b) Δτ = 5 JahreDa hier die Koordinatenzeit unbekannt ist, müssen wir nach ihr auflösen:
(2) Δt = Δτ⁄√{1 − v²⁄c²} = Δτ∙γ
Dabei ist γ einfach der Kehrwert von obigen 0,5426, was etwa 1,843 ist. Als Ergebnis kommen hier etwa 9,2 Jahre heraus.
--------
¹) Selbstverständlich muss sie ihre Geschwindigkeit (engl. velocity) geändert haben, deren Betrag das Tempo ist – sonst hätte sie sich nur immer weiter entfernt – aber nur ihrer Richtung nach.