Wieso kann ich diesen Bruch nicht kürzen (Wurzeln)?
Hey, es geht um folgende Rechnung:

Ich habe die Aufgabe davor selbst mal durchgerechnet und dabei im Zähler und Nenner des Bruchs den Faktor 2 weggestrichen.
Dabei käme dann folgender Term heraus:
√2 + (√2 + 3)
Nun dachte ich mir, dass ich vielleicht einfach nicht klug umgeformt habe und der Dezimalwert letztlich aber derselbe sein könnte.
Gebe ich jedoch die Terme des Lösungsweges und meines Terms in den Taschenrechner ein, kommen dabei sehr unterschiedliche Ergebnisse heraus. Also ist das so ja scheinbar nicht möglich. :D
Kann mir bitte jemand erklären, wieso das nicht geht und was mein Fehler war?
2 Antworten
weiß nicht genau was du meinst
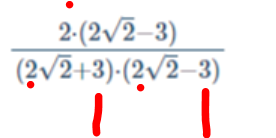
wenn es diese Zweien sind , dann kann man da nur kürzen ,wenn auch bei +3 und -3 eine 2 hat
.
ergänzung
würde man die 2 im Zähler ausklammern , bliebe im Nenner 2* ( w(2)+1.5 ) * 2 * ( w(2) - 1.5 ) übrig
was zu
4 * (2 - 2.25) führt = -1
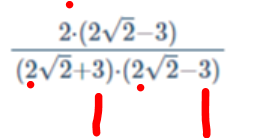
Im Nenner steht eine Summe. Du müsstest die 3 ebenfalls durch 2 dividieren. Außerdem bleibt der Nenner unter dem Bruchstrich.
Aus Summen darfst du nicht kürzen, nur aus Produkten.
Ein Beispiel mit einfachen Zahlen:
2/(2+4) wäre nach deiner Methode 1/(1+4)=1/5.
Aber 2/(2+4)=2/6=1/3 .
Alles klar! Also darf ich grundsätzlich nicht kürzen, wenn im Nenner oder Zähler ein Strich-Rechenzeichen vorkommt, auch wenn dabei mehrere Faktoren auftauchen, die nicht direkt in die Strichrechnung "verwickelt" sind?
Du darfst aber jeden Summanden durch die Kürzungszahl dividieren. Bei meinem Beispiel:
2/(2+4)=1/(1+2)=1/3
Danke, bei dem Bruchstrich fällts mir jetzt wie Tomaten von den Augen... :D
Zu der 3: Wieso müsste ich die ebenfalls dividieren? Einzelne Faktoren über und unterhalb des Nenners darf man doch wegkürzen, oder? Sprich bei 2 / (2 * √2 + 3) hätte ich im Nenner dann einmal den Faktor 2 und noch den Term mit der Wurzel und würde dann oben und unten einmal die 2 wegstreichen, hätte dann jedoch nicht wie von mir formuliert nicht √2 + 3 sondern 1 / (√2 + 3). Macht das Sinn, oder wieso muss ich an dieser Stelle die 3 noch kürzen? :D