Wieso ist das falsch / Horner Schema?
Hallo,
Bin für jeden Tipp sehr dankbar.
Wieso funktioniert das nicht am Ende muss ja 0 rauskommen?
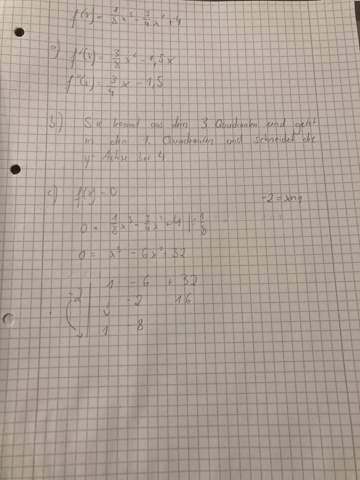
1 Antwort
Du hast einen Fehler gemacht (siehe unten in meiner Antwort).
Das Horner-Schema kurz erklärt:
a_n x^n + a_(n–1) x^(n–1) + a_(n–2) x^(n–2) + ... + a_1 x + a_0
= ((...(((a_n x + a_(n–1)) x + a_(n–2)) ... ) x + a_1) x + a_0
Bedeutet fürs Kopfrechnen
a_n • x
+ a_(n–1)
• x
+ a_(n–2)
• x
+ a_(n–3)
...
• x
+ a_1
• x
+ a_0
In unserem Fall also
x³ – 6 x² + 32
= ((1 x – 6) x + 0) x + 32
Du musst also rechnen
1 • (–2) | 1 • (–2) = –2
–6 | –2 – 6 = –8
• (–2) | –8 • (–2) = 16
+ 0 | 16 + 0 = 16
• (–2) | 16 • (–2) = –32
+ 32 | –32 + 32 = 0
Also ist –2 tatsächlich eine Nullstelle.
Das Horner-Schema ist also, wenn in der ersten Zeile die Koeffizienten stehen, immer oben links zu beginnen.
Koeffizient oben links, dann diagonal rechts runter, also • x, dann Koeffizient über x, also + Koeffizient.
Dann wieder diagonal runter, • x, und wieder + den darüber liegenden Koeffizienten.
Du hast allerdings den Fehler gemacht, den Koeffizienten für den linearen Teil null zu setzen. Nach deinem Schema würde es sich um die Funktion 1 x² – 6 x + 32 handeln, aber es ist ja eigentlich x³ – 6 x² + 32. In der ersten Zeile müsste also stehen
1, –6, 0, 32.
Es ist wichtig, dass du das dazu schreibst! Das musst du immer machen, wenn eine Potenz von x fehlt.
Z. B. müsste die erste Zeile des Horner-Schema für die Funktion 2 x⁴ + 4 x heißen
2, 0, 0, 4, 0,
weil x³, x² und x⁰ fehlen.
Danke ich habe es auch jetzt richtig gemacht es lag also daran, dass ich die 0 weggelassen habe. Danke 🥰