Wie lese ich aus einem Funktionsgraphen 4. Grades die Funktionsgleichung ab?
5 Antworten
Wenn du weißt dass es eine Funktion 4ten Grades ist ist die Funktionsgleichung direkt aus den Nullstellen ablesbar. Da hier wirklich 4 Nullstellen vorliegen sind alle Reell und daher ablesbar daher gilt f(x)=(x-x0)*(x-x1)... wobei x0 x1 usw die Nullstellen des Polynoms sind.
In deinem Fall ergibt sich die Funktion zu f(x)=(x+2)*(x-0)*(x-2)*(x-4)*a wobei a ein Faktor ist mit dem du die Höhe der Funktion noch angleichen musst.
Keine Ahnung wie man in der Angabe auf den Faktor kommt da wir aber nicht das komplette Beispiel sehen kann der ja durchaus wo dabei stehen oder es die Lage oder zumindest Höhe eines Extremwertes oder ähnliches gegeben.
Ich würd ihn aber pi mal Daumen auf 0.1 Schätzen, dann passts so ziemlich zum Graphen.
Aso ja in den Bsp reichts die Ableitung bei x=1 Null zu setzen.
Manchmal sieht den Wald vor lauter Bäumen nicht.
Aber dann reicht ein kleiner Klapps auf den Hinterkopf und schon gehts :-).
Ablesen genau gar nicht.
Du kannst die Nullstellen ablesen, globales Verhalten, Y Achsenabschnitt, du siehst das nicht alle Exponenten gerade sind
Bei den Nullstellen auf Vorzeichenwechsel achten.
Dann hast du schon die Hälfte der Gleichung, dann fehlt noch evtl. a
Hallo,
Allg Formel: y=ax^4+bx^3+cx^2+dx+e
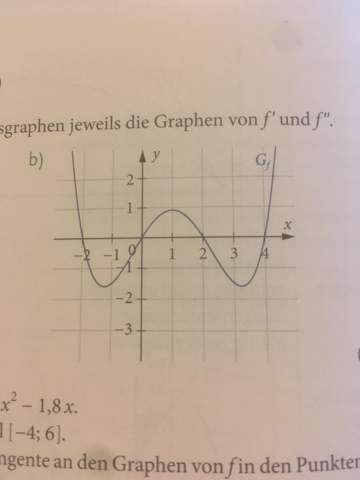
Also, du kannst folgende Punkte (x,y) ablesen: (-2,0), (0,0), (2,0), (4,0). Jetzt setzt du diese Punkte in die allg Formel und hast dann 4 Gleichungen. Mit LGS kannst du es dann lösen um die Werte für a,...,e zu bestimmen.
Das LGS ist allerdings mit den von dir genannten Punkten unterbestimmt. Man braucht noch mindestens einen weiteren Punkt. Da man aus den Nullstellen alleine nur das normierte Polynom erzeugen kann, welches dann noch mit einem Faktor skaliert werden muss.
Zuerst schätzen wir den Grad der Funktion ab.
Sowohl die Anzahl von 4 Nullstellen als auch die parabolische Form für große x spricht für eine Funktion 4. Grades.
Dafür setzen wir die allgemeine Nullstellenform an:
f(x) = a * (x + 2) * x * (x - 2) * (x - 4)
und multiplizieren aus:
f(x) = a * (x^2 + 2x) * (x - 2) * (x - 4)
= a * (x^3 + 2x^2 - 2x^2 - 4x) * (x - 4)
= a * (x^3 - 4x) * (x - 4)
= a * (x^4 - 4x^2 - 4x^3 + 16x)
= a * (x^4 - 4x^3 - 4x^2 + 16x)
Nun fehlt uns noch der Faktor a. Um den zu lösen, brauchen wir einen zusätzlichen Wert. Da mache ich es mir einfach und verwende den Punkt (1/1):
1 = a * (1 - 4 - 4 + 16) = a * 9
a = 1/9
Die Funktion hat also die Gleichung:
f(x) = 1/9 x^4 - 4/9 x^3 - 4/9 x^2 + 16/9x
Zur Kontrollle gebe ich nun diese Funktion in einen GTR ein und gucke, was rauskommt:

...das sieht doch gut aus.

Findest du denn irgendwelche besonderen Punkte, deren Koordinaten sich leicht ablesen ließen?
Den du aber nicht genau ermitteln kannst.
Es ergibt sich, wenn man die
Funktion um 1 nach links verschiebt,
(x+3)*(x+1)*(x-1)*(x-3)
Binomische Formeln:
(x^2-9)*(x^2-1)
und
x^4 - 10x^2 + 9
Verschiebung rückgängig:
(x-1)^4 - 10(x-1)^2 + 9
Stimmt alles bis auf den Faktor.
Aber wie willst du den bestimmen?