Wie kann ich zu dieser Funktionsgleichung eine ganzrationale Funktion bestimmen?
Hallo,
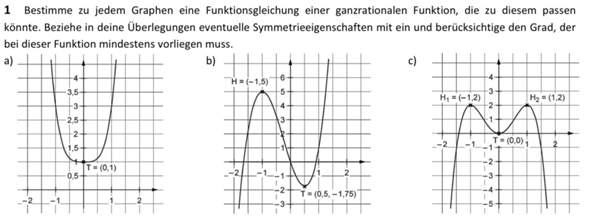
ich schreibe morgen eine Mathe Klausur und bin gerade am lernen. Kann mir wer Schritt für Schritt erklären wie Aufgabe 1b funktioniert, da ich diese nicht hinbekomme. Aufgabe und Lösungen (aber der Rechenweg halt nicht) sind im Anhang.
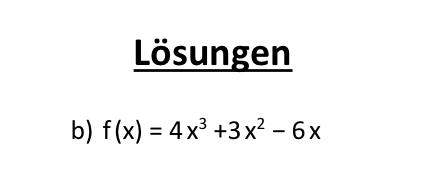
4 Antworten
Bei der Aufgabe b) sehe ich keine andere Möglichkeit als aus den Bedingungen
mit Hilfe der allgemeinen Funktion für eine ganzrationale Funktion dritten Grades (das kann man dem Funktionsverlauf entnehmen)
ein Gleichungssysten zu erstellen. Dabei kann man Gleichung (1) sofort zu d=0 verwenden.
Tipps:
- Zur Bestimmung eine ganzrationalen Funktion n-ten Grades solltest du n+1 Punkte auf dem Graphen kennen.
- Ob eine Funktion gerade oder ungerade (n ist entsprechend gerade bzw. ungerade) ist, sieht man am Symmetrieverhalten.
- Stellen bei x=0 oder y=0 eignet sich gut als Punkte, an denen man sich orientieren kann.
- Du musst eine Gleichung mit n + 1 Variablen aufstellen, um die Aufgabe zu lösen.
- Du erhälst diese Gleichung, wenn du dir klar machst, wie die allgemeine Form einer ganzrationalen Funktion n-ten Grades aussieht.
Für symmetrische Funktionen in Bezug auf die y-Achse muss man die Potenz von x geradzahlig ansetzen, für unsymmetrische ungeradzahlige.
Gleichung dritten Grades, Du brauchst also 4 Informationen.
Du hast den Funktionswert an zwei Punkten und den Wert der ersten Ableitung an zwei Punkten.
Dann das altbekannte Schema abarbeiten.
Zeig am besten Deinen Rechenweg, dann können wir Dir Deine/n Fehler zeigen.
Ja, das hab ich auch gemacht nur waren die Werte die in meinem Taschenrechner rauskamen nicht die Lösung, deshalb wollte ich hier mal Nachfrage, um den Rechenweg zu bekommen.