Wie kann ich anhand des Graphen den Funktionsterm bestimmen? Kann mir jemand 15a) erklären?
Normalerweise schaue ich immer auf Eigenschaften wie Nullstellen, Asymptoten, grenzwertverhalten etc. Hier steht aber was von aufstellen und lösen eines göeichungssystems, anders geht es wohl nicht..
(siehe 15a)
Ich bitte um schnelle Antworten, ich schreibe morgen Schulaufgabe :(

3 Antworten
Gg:
Zuerst suchen wir den Ansatz. Wir sehen, dass es sich um eine Parabel handelt und setzen daher an:
f(x) = ax^2 + bx + c
und setzen der Reihe nach die Punkte ein:
a - b + c = 5,5
c = 3
4a + 2b + c = 4
Wenn wir c = 3 einsetzen:
a - b + 3 = 5,5
4a + 2b + 3 = 4
Gl. 1 nach a auflösen:
a = 2,5 + b
in Gl. 2 einsetzen:
10 + 4b + 2b + 3 = 4
nach b auflösen:
6b = -9
b = -3/2
daraus folgt:
a = 2,5 - 3/2 = 1
Lösung:
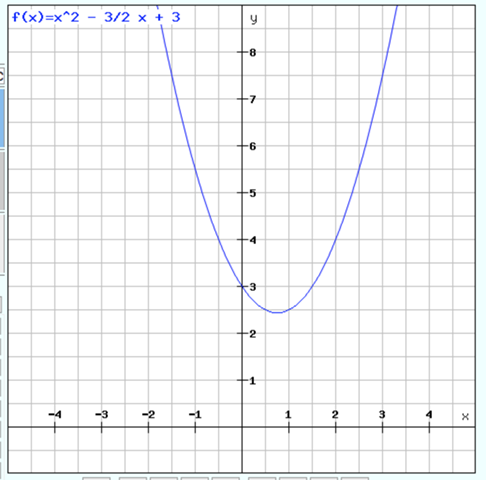
f(x) = x^2 - 3/2 x + 3

f(x) = (-3/2) * (x + (1/2)) * (x - (5/2)) / (x - (1/20))
Wie komme ich an diese Funktionsgleichung?
Die Nullstellen liegen bei x_1 = -1/2 und bei x_2 = 5/2. Das führt zu den Linearfaktoren (x + (1/2)) * (x - (5/2)) im Zähler.
Die rot gestrichelte Linie ist die Asymptote. Diese hat die Funktionsgleichung y_A = (-3/2) * x + 3. Damit liegt der Faktor (-3/2) fest.
Eine Polstelle ist vorhanden. Es ist nicht ersichtlich, ob bei x = 0 eine Polstelle ist bzw. ob diese geringfügig verschoben ist. Daher setze ich P (-1│2,5) ein um die Verschiebung zu ermitteln.
2,5 = (-3/2) * (-1 + (1/2)) * (-1 - (5/2)) / (-1 - b)
-5/3 = (-1/2) * (-7/2) / (-1 - b)
(-5/3) * (-1 - b) = 7/4
-1 - b = -21/20
b = 1/20
Die Funktionsgleichung der Parabel hat Hamburger02 bereits bestimmt. Damit sind beide Funktionsgleichungen bekannt und die Lösungen für b) - d) können bestimmt werden.
g ist eine Parabel
ax² + bx + c
mit den Punkten auf ihr stellt man drei Glg auf
(2/4)
4 = a*2² + b*2 + c
aus denen bestimmt man a , b und c
.
f eine Hyperbel
aus
(3-0)/(0-2) = m
-3/2 x + 3 = f(x) die Asymptote bestimmen
.
a/x - 1.5 x + 3 = f(x)
(-1/2.5) nutzen für a
a/-1 - 1.5*-1 + 3 = 2.5
-a + 1.5 + 3 = 2.5
-a = -2
a = +2