Wie ist das Zwillingsparadoxon lösbar?
Trotz einiger Internetbeiträge und Wikipedia verstehe ich die Auflösung des Zwillingsparadoxon leider immer noch nicht:
Die Zeitdilatation wurde ja mit Atomuhren im Experiment real nachgewiesen. Nur flogen dabei die bewegten Uhren nicht geradelinig von der ruhenden Uhr weg, sondern einmal um die Erde.
Ebenso können wir ja mal annehmen, dass der in einer Rakete mit annähernder Lichtgeschwindigkeit reisende Zwilling nicht geradelinig zu einem fernen Stern fliegt, dort umdrehen muss und dann zurück fliegt, sondern er ebenfalls eine große Kreisbahn fliegt (Durchmesser einige Lichtjahre), bis er wieder zum Zwillingsbruder zurück kommt.
Vernachlässigen wir einfach auch mal die dann nur noch zwei nötigen Beschleunigungs- und Bremsphasen (jeweils eine).
Im Bezugsystem des reisenden Zwillings bewegt sich die Erde mit annähernder LG einmal auf einer Kreisbahn, die wieder bei ihm endet, und im Bezugsystem des Bruders auf der Erde bewegt sich der Zwilling mit annähernder LG einmal auf einer Kreisbahn, die wieder bei ihm endet.
Von beiden aus gesehen, altert der jeweils andere langsamer, womit wir bei der paradoxen Situation wären, dass beim abschließenden Treffen der jeweils Andere jünger geblieben sein müsste.
Wie ich aber überall lese, ist nach der Reise aber tatsächlich nur der in der Rakete reisende Bruder jünger.
An welcher Stelle sind die beiden Bezugsysteme nicht gleichberechtigt, und wie wird das Paradoxon letztlich wirklich vermieden? Leider verstehe ich es immer noch nicht...
4 Antworten
die im jeweiligen Bezugssystem spürbaren Beschleunigungskräfte sind komplett unterschiedlich. Sind beide Schiffe im Weltraum, dann könnte das eine komplett in der Schwerelosigkeit verharren, und das würde man als Passagier auch merken.
Würde das andere für die Reise jeweils mit 1g Beschleunigen bzw. Bremsen, dann wäre das der Unterschied.
sondern er ebenfalls eine große Kreisbahn fliegt (Durchmesser einige Lichtjahre)
Eine Kreisbahn ist doch immer eine beschleunigte Bewegung - während der ganzen Zeit - selbst bei gleichbleibender Geschwindigkeit.
https://de.wikipedia.org/wiki/Hafele-Keating-Experiment
An welcher Stelle sind die beiden Bezugsysteme nicht gleichberechtigt
Die Uhr auf der Kreisbahn wechselt stetig ihr Inertialsystem.
Entscheidend ist, dass der Reisende ganz eindeutig ein Reisender ist, weil er nicht inertial ist. Er beschleunigt, wenn er sich auf einer Kreisbahn bewegt, ununterbrochen in Richtung Mittelpunkt des Kreises.
Wenn wir von „dem Ruhesystem“ des Reisenden reden, so ist dies ein Nichtinertialsystem, nämlich ein mit einer Winkelgeschwindigkeit ω rotierendes Koordinatensystem, in dem es ein Zentrifugalpotential gibt, bei dem eine im Abstand r vom Kreismittelpunkt mit –ω (relativ zum System) bewegte Uhr genau so schnell läuft wie die im Mittelpunkt, während eine bei r (relativ zum System) stationäre Uhr langsamer läuft.
Die in einem rotierenden Koordinatensystem auftretenden Trägheitskräfte (Zentrifugal- und Coriolis-) wirken nämlich genau wire Gravitation, und auch die verlangsamt die Zeit.
Unter einem Paradoxon versteht man eine Situation, die widersprüchlich erscheint, da man sie nicht voll verstanden hat (also Denkfehlern aufsitzt). Tatsache ist:
Wenn Zwillinge sich von einander weg bewegen, wird jeder der beiden den Eindruck haben, die Zeit des jeweils andere verginge langsamer. Tatsächlich aber altern sie gleich schnell, solange sie gleicher oder gar keiner Beschleunigung unterliegen.
Erst wenn Zwillinge unterschiedlich starker Beschleunigung — bzw. unterschiedlich starker Gravitation — ausgesetzt sind, kommt ein Altersunterschied zustande, der auch dann noch gegeben sein wird, wenn sie sich wieder treffen und relativ zu einander NICHT mehr bewegt sind.
Beide Aussagen sind richtig, aber nur die erste ist einfach einzusehen. Sie resultiert aus der Endlichkeit der Lichtgeschwindigkeit und der Tatsache, dass wir alles, was wir geschehen sehen, als eben jetzt geschehend einstufen.
Die zweite Aussage ist richtig, da unterschiedlich beschleunigte Objekte die Raumzeit auf unterschiedlichen "Wegen" durchqueren und diese Wege umso kürzer sind, je stärker das Objekt beschleunigt ist.
Hmmm.. Muss ich erst noch sacken lassen, aber trotzdem danke schon mal für die Antwort auf meine doch schon ältere Frage! :)
LiHallo Mannimanaste,
…annähernder Lichtgeschwindigkeit…
die Lichtgeschwindigkeit ist eigentlich ein Tempo (engl. speed), also nur der Betrag einer Geschwindigkeit (engl. velocity), welche ihrerseits eine Vektorgröße ist, eine Größe mit Richtung, und sie wird gewöhnlich mit c bezeichnet. Das sollten wir auch tun.
Die Zeitdilatation wurde ja mit Atomuhren im Experiment real nachgewiesen.
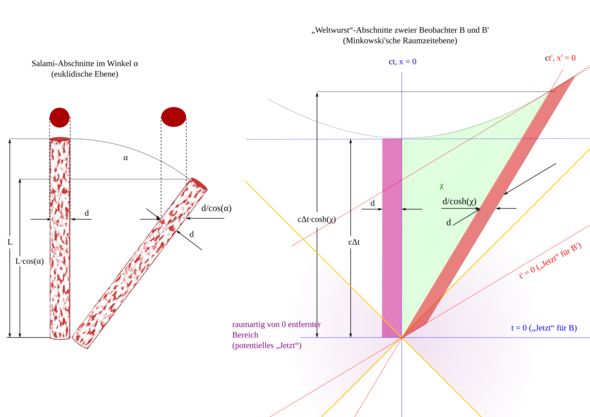
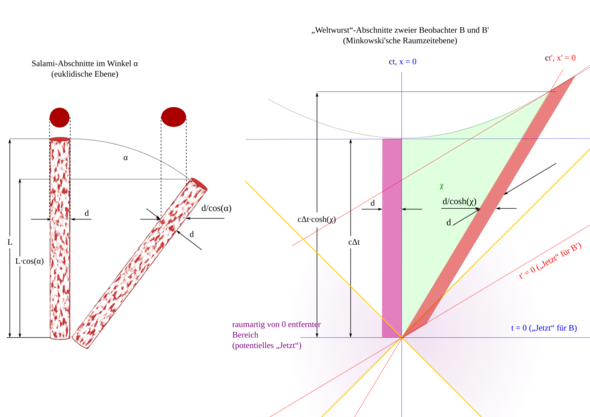
Das Wort „Zeitdilatation“ ist irreführend. Da wird nichts auseinander gezogen oder dergleichen mehr, sondern das ist eigentlich ein Projektionseffekt, ähnlich dem, den Du hast, wenn Du eine Salami der Länge L mit dem hinteren Ende an eine andere gleich lange oder ein Lineal legst, aber nicht gerade, sondern schräg in einem Winkel θ. Die Richtung des Lineals nenne ich im Folgenden z-, die quer dazu x-Richtung.
Selbstverständlich wird das vordere Ende, wenn man es senkrecht auf's Lineal oder die andere Salami projiziert, bei
(1) Δz = L·cos(θ)
und nicht bei L liegen, und da würde kein Mensch von „Längenkontraktion“ reden.
In der räumlichen Ebene ist
(2) L² = Δx² + Δz²,
unabhängig von der Lage der Salami. In einer Raumzeit-Ebene ist hingegen
(3) Δτ² = Δt² – Δx²/c² = Δt²(1 – v²/c²),
d.h., eine Zeitspanne der Dauer Δτ auf der Uhr eines Beobachters A dauert auf der Uhr eines relativ zu A mit v bewegten Beobachters B länger statt kürzer, denn
(5) Δt² = Δτ²/(1 – v²/c²) =: Δτ²·cosh(χ).
An die Stelle von θ tritt hier die Rapidität χ, an die des Cosinus der Cosinus Hyperbolicus, alles wegen des Minuszeichens in Gleichung (3), die garantiert, dass etwas, das sich relativ zu A (wenn der als ruhend gilt) mit c bewegt, das auch tut, wenn B als ruhend und A als mit –v bewegt gilt.
Das ist nämlich die Grundlage der Speziellen Relativitätstheorie und beruht komplett auf Galileis Relativitätsprinzip, denn c ist nicht einfach irgendein Tempo, sondern beruht komplett auf den Gesetzen der Elektrodynamik, die J.C.Maxwell Mitte des 19. Jahrhunderts formuliert hat. Daher muss c absolut sein.
Aber zurück: Krumme zeitartige Wege sind wegen des Minuszeichens in (3) kürzer statt gerade, und A als jemand, der eine konstante Geschwindigkeit hat, fährt einen geraden Weg durch die Raumzeit, auch wenn diese nicht 0 sein sollte (s. 2. Bild, mit verschiedenen ,,offset-Geschwindigkeiten")
Im Bezugsystem des reisenden Zwillings bewegt sich die Erde mit annähernder LG einmal auf einer Kreisbahn, die wieder bei ihm endet,…
Eben nicht, denn - solange wir das Problem mit der SRT behandeln - gibt es gar nicht das Bezugssystem von B, denn als Bezugssystem ist nur ein Inertialsystem zulässig, und dies darf nicht z.B. ein rotierendes sein.
Wenn Du von dem Bezugssystem von B sprechen willst, musst Du schon Allgemeine Relativitätstheorie betreiben, und da treten Zentrifugal- und Coriolisterme auf, die der Gravitation äquivalent sind. B befindet sich do betrachtet auf niedrigerem Gravitationspotential als A.


Ja und? Gibt's bei beschleunigten Bewegungen keine Zeitdilatation? Dann dürfte das Uhrenexperiment ja auch nicht geklappt haben, als man eine Atomuhr mit einem Flugzeug um den Globus herum flog, die danach um einige Nanosekunden (oder Bruchteile einer Nanosekunde?) langsamer ging, als die stationäre Uhr, die man am Flugplatz ließ. Das war ja ebenfalls eine Kreisbahn.