Wie erkenne ich aus diesen Funktionen deren zugehörigen Graphen?
Das sind die Funktionen:
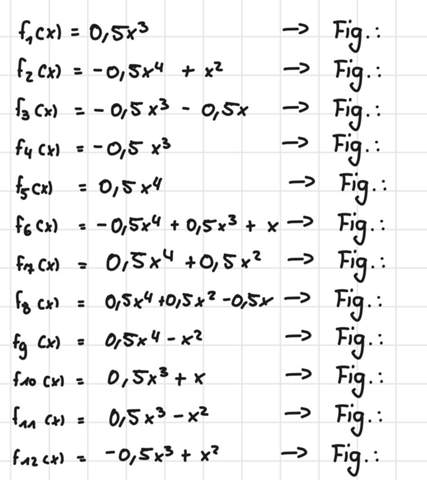
Und das sind die Graphen die man den Funktionen zuordnen muss:
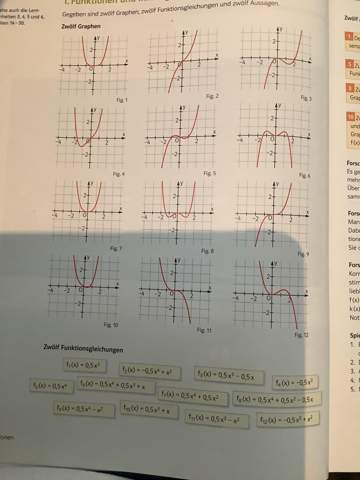
Ich möchte nicht das mir irgendwer die Aufgaben vorsagt oder so, ich wollte nur fragen ob mir jemand erklären könnte wie ich aus dieser Art von Funktionen den Graphen ablesen kann.
das einzige was ich weiß ist das wenn die Exponenten gerade sind das quasi wie so n u geformt ist bzw. Beide enden sich unendlich lang in eine Richtung strecken wie zum Beispiel bei Graph 1 und bei ungerade exponenten sieht’s dann wie bei Graph 2 zum Beispiel aus, da endet mein Wissen aber auch
Ich wollte nur fragen*
2 Antworten
Dass das Verhalten für betragsmäßig große x (" |x| -> unendlich ") nur vom Vorfaktor des höchsten Exponenten abhängt, weißt du ja schon.
Ebenso, was es bedeutet, ob der höchste Exponent gerade oder ungerade ist.
Das Einsetzen von ein paar Testwerten für x hat fabrie schon genannt.
Für betragsmäßig kleine x wird das Verhalten nur vom Vorfaktor des kleinsten Exponenten bestimmt. (Falls der kleinste Exponent 0 ist, ist das eine konstante Verschiebung in y-Richtung - dieser Fall kommt hier nicht vor -, aber man sieht dort immer noch das typische Verhalten des zweitkleinsten Exponenten.)
Beispiel: Der Graph von Fig. 1 ist unten deutlich flacher als eine Parabel. Hier kann also kein x² auftreten.
In Fig. 3 und Fig. 12 haben wir in der Nähe der 0 ungefähr eine Parabel. Hier kommt also ein x² vor. Vorzeichen je nach Öffnungsrichtung der Parabel.
Einige Graphen sind in der Nähe von 0 einer geneigten Geraden sehr nahe. Das spricht für einen Faktor x^1.
Damit solltest du hier weiterkommen.
Wenn man den Funktionsterm leicht faktorisieren kann oder/und Nullstellen "sieht", hilft das auch weiter. Wenn man z. B. ein (x-2)^2 ausklammern kann, verhält sich der Graph in der Nähe von x=2 wie eine Parabel.
Da gibt es mehrere Möglichkeiten. Einerseits könntest Du für f(x) einen beliebigen X-Wert einsetzen, um somit f(x) herauszufinden. Das geht am besten mit einer Wertetabelle. Der Aufwand ist groß, aber diese Methode ist immer idiotensicher.
Dann verrät Dir das Vorzeichen vor dem x, ob der Graf steigt oder fällt. Du hast 3 mal ein - vor den Gleichungen, dementsprechend gibt es auch 3 fallende Grafen, was der Fall ist.
Ich probiere die Methode mit dem beliebigen x wert mal aus, danke