Wie berechnet man die c (1)?
1 Antwort
Unter a) steht die Formel für den Abstand zweier Punkte. Bei c) hast Du nun zum einen den Punkt der Funktion (x|f(x)) und den Punkt Q(x_q|y_q).
Setzt Du diese Koordinaten nun in die rechte Seite dieser Gleichung ein, erhältst Du einen Term, der von x abhängt. Dies ist dann quasi der Term der "Punktabstandsfunktion". Davon musst Du nun das Minimum bestimmen...
c(1): hier gilt bezogen auf die unter a) genannte Gleichung:
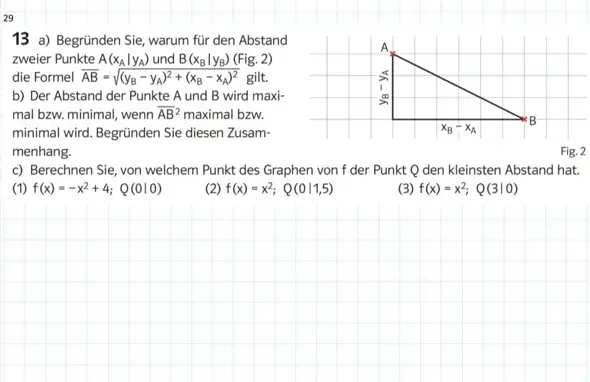
x_A=0; y_A=0; x_B=x; y_B=-x²+4
Das jetzt in die Gleichung eingesetzt (ich nenne die Funktion mal d wie distance...)
=> d(x)=Wurzel((-x²+4)-0)²+(x-0)²)=Wurzel((-x²+4)²+x²)
Das nun evtl. noch unter der Wurzel ausmultiplizieren und dann die Extremstellen bestimmen, wovon das/die Minimum/Minima gesucht ist/sind.
Richtig, d. h. aus (-x²+4)² wird +x⁴-8x²+16 (wenn die Frage darauf bezogen war).
Wenn man minus x² quadriert, dann ist das doch positiv oder?