Fehlende Größen in einem Viereck berechnen?
Hallo,
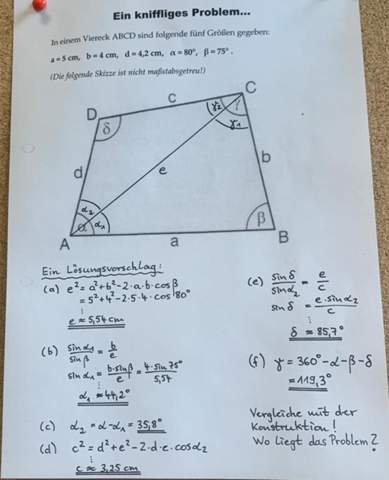
Ich brauche dringend Hilfe. Ich habe hier die Lösungen einer Aufgabe, wo man die fehlenden Größen in einem Trapez berechnet soll, da habe ich ja auch alles richtig nun steht da jetzt aber die Frage : Vergleiche mit der Konstruktion. Wo liegt das Problem? Kann mir da jemand helfen. Ist das vllt. so weil der Winkel Gammer nicht stumpfwinklig abgebildet ist?....
Schon im voraus vielen Dank für Antworten :)
LG wanja
2 Antworten
δ stimmt nicht. Und damit auch γ.
Gegeben sind ja die roten Maße (siehe Bild)
Ich hab wie folgt gerechnet.
---
e² = a² + b² - 2 * a * b * cos(β)
e² = 5^2 + 4^2 - 2 * 5 * 4 * cos(75)
e = Wurzel( 5^2 + 4^2 - 2 * 5 * 4 * cos(75) )
e = 5,54 cm
---
sin(α1) / sin(β) = b / e
sin(α1) = ((b * sin(β)) / e)
sin(α1) = ((4 * sin(75)) / 5,54)
sin(α1) = 0,6974193692
α1 = 44,2°
---
α2 = α - α1
α2 = 80 - 44,2
α2 = 35,8°
---
c² = d² + e² - 2 * d * e * cos(α2)
c² = 4,2^2 + 5,54^2 - 2 * 4,2 * 5,54 * cos(35,8)
c² = 63,33708557
c = Wurzel( 4,2^2 + 5,54^2 - 2 * 4,2 * 5,54 * cos(35,8) )
c = 3,25 cm
------
δ = ARCCOS( (e² - c² - d²) / (-2 * c * d) )
δ = ARCCOS( (5,54^2 - 3,25^2 - 4,2^2) / (-2 * 3,25 * 4,2) )
δ = 95,2°
---
γ = 360 - α - β - δ
γ = 360 - 80 - 75 - 95,2
γ = 109,8°
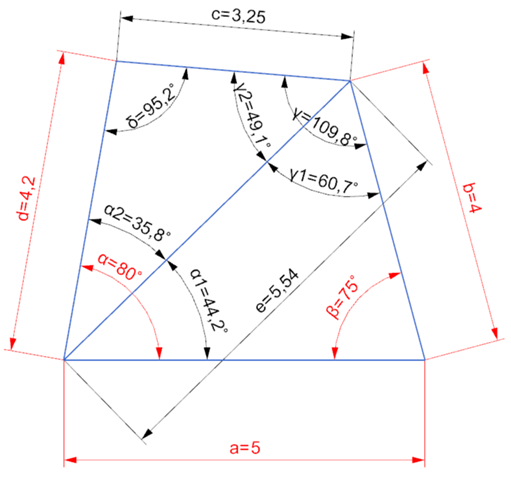
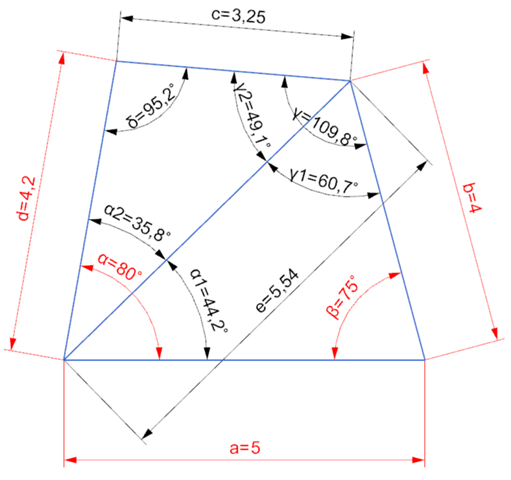
Der Sinussatz kann tückisch sein:
Bei e) folgt aus sin(Delta) = 0,007 nicht zwingend Delta = 85,7°.
Es können auch 180° - 85,7° = 94,3° sein.
Bei b) tritt dieses Problem nicht auf.
Es ist zwar als zweite Lösung 180° - 44,2° = 135,8° denkbar, aber mit Beta zusammen wird die Innenwinkelsumme im Dreieck ABC größer als 180".