Wie beeinflussen C (Kapazität) und L (Induktivität) den Widerstand?
Thema: Spule und Kondensator im Wechselstromkreis
Meine Frage: Wie beeinflussen C (Kapazität) und L (Induktivität) den Widerstand?
Und falls möglich kann es mir auch jemand begründen?
5 Antworten

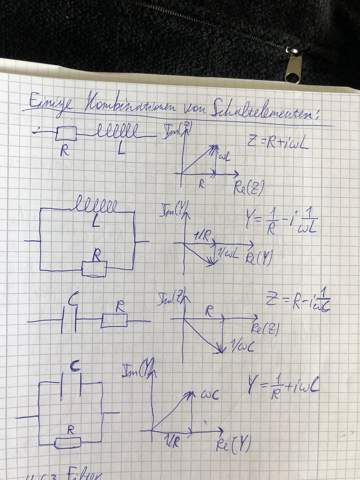


In einer Reihenschaltung von U (Spannungsquelle), R (Wirkwiderstand), L (Spule) und C (Kondensator), haben L und C keinen Einfluss auf R.
Es gibt allerdings noch den Blindwiderstand Z. Dieser entsteht durch die Selbstinduktion von Spule und Kondensator. Z ist eine konplexe Zahl. Für einen Bandpassfilter gilt: Z = R - i / ωC + iωL.
Dabei ist i die komplexe „Einheit“ und ω ist die Frequenz des Wechselstroms in dieser Schaltung.

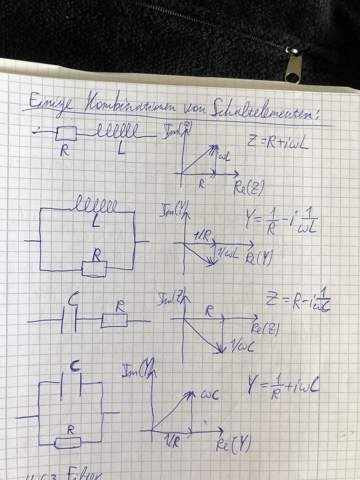


Die Reaktanz beider Bauteile ist definiert durch:
- X_L = wL
- X_C = 1/wC
w ist die Kreisfrequenz Omega und somit frequenzabhängig von der Quelle. C und L sind die Bauteilgrößen Kapazität und Induktivität und bauteilabhängig und damit (ideal) konstant.
Somit hängt der Wechselstromwiderstand idealer Bauteile (ohne parasitäre Widerstände realer Bauteile) nur von der Frequenz ab.
Die Kapazität und die Spule sind sogenannte "komplexe widerstände" der widerstand der induktivität berechnet sich folgendermaßen:
iXL=L*2*pi*f
Er ist also proportional zur Frequenz der Spannung. Da die Frequenz einer gleichspannung 0 ist, ist auch der Widerstand 0. Das i deutet auf eine imaginäre Zahl Wurzel-1 als Faktor siehe (gaußsche zahlenebene).
Bei der Kapazität sieht es wie folgt aus:
iXC=1/C*2*pi*f
Auch hier eine imaginäre Zahl. Der Widerstand der Kapazität ist also antiproportional zur Frequenz.
Da die Frequenz bei der gleichspannung 0 ist, ist der Widerstand nahezu unendlich groß.
Wie man sieht entwickeln die komplexen Widerstände erst bei wechselspannung ihren Widerstand.
Bei der induktivität kommt durch der ständigen elektrischen flussänderung zu einer selbstinduktion, welcher der angelegten Spannung entgegen wirkt. Auf diese Weise kommt es zu dem Widerstand. Hat die Spannung sein Maximum erreicht kommt es zu keiner weiteren Änderung mehr und es beginnt ein Strom zu fließen.
Dies führt nun dazu, dass Strom und Spannung nicht mehr phasengleich verlaufen sondern bei einer idealen induktivität um 90° versetzt sind.
Um das Phänomen nun zu erklären und berechnen zu können nutzt man die gaußsche zahlenebene. Diese art der Rechnung nennt sich "komplexe Wechselstromrechnung"
Diese phasenverschiebung führt zu Problemen im Netz, da es zu einer negativen Leistung kommt.
P=U*I ist Strom und Spannung in Phase so besitzen sie zu jederzeit das gleiche Vorzeichen
+*+=+
-*-=+
Die Leistung ist zur jederzeit positiv. Kommt jedoch eine phasenverschiebung ins Spiel kommt es zu unterschiedlichen Vorzeichen und die Leistung hat ein negatives Vorzeichen.
Das bedeutet es kommt zu einer sogenannten Blindleistung die kompensiert werden muss, da die Blindleistung das Netz nur belastet ohne etwas zu bewirken, was dazu führt, dass größere Querschnitte verlegt werden müssen.
Ah danke für den Hinweis. Kleiner Flüchtigkeitsfehler meiner Seite.
Es ist wichtig, ob L und C in Reihe geschaltet sind, oder parallel. In beiden Fällen verhält sich der Gesamtwiderstand - als Funktion der Frequenz - ganz unterschiedlich (Resonanzeffekte).
Allerdings nur wenn hier der Scheinwiderstand gemeint ist. Der Wirkwiderstand ist unabhängig davon.
Ja, aber wenn nach dem Einfluss von L und C in einem WECHSELstromkreis gefragt wird, dann handelt es sich logischerweise um die Frequenzabhängigkeit, oder?
Es ist aber nicht klar was hier als Widerstand bezeichnet wird. In einem Wecheslstromkreis gibt es nicht nur den Widerstand sondern eben einen Wirkwiderstand, eine Scheinwiderstand und einen Blindwiderstand.
Auf den Wirkwiderstand im Wechselstromkreis hat der Wert von L und C gar keinen Einfluss, nur auf den Blindwiderstand und den Scheinwiderstand, auf den Blindwiderstand hat wiederum ein ohmscher Widerstand keinen Einfluss.
Man muss also hier auch dazu sagen welchen dieser 3 Widerstände man hier betrachtet. Ich würde natürlich auch mal annehmen dass hier der Scheinwiderstand gemeint ist, nur sollte mans eben auch dazu schreiben, dass man eben jetzt vom Scheinwiderstand spricht.
Wenn du mit Widerstand den Wirkwiderstand meinst, dann beeinflussen ideale Kapazitäten und Induktivitäten diesen gar nicht.
Die Kapazitäten haben aber über Xc = 1/(jwC) so wie die Induktivitäten über XL = jwL einen Beitrag zum Blindwiderstand und zum Scheinwiderstand.
Ich meine den elektroschen Widerstand in einem Wechselstromkreis
Schon klar, aber da gibt es 3 verschiedene Widerstände. Den Wirkwiderstand, den Blindwiderstand und den Scheinwiderstand.
Es ist also hier die Frage welchen dieser 3 Widerstände du mit "elektronischer Widerstand" bezeichnest.
Achso, mh das weiß ich nicht genau in der Schule reden wir immer nur von elektrischem Widerstand :/
Wenn du den Scheinwiderstand meinst dann gilt:
Z = R + jX
j ist dabei die Imaginäre Einheit.
Kondensatoren und Induktivitäten können jetzt nur auf den Term mit jX wirken. So hat zB eine Serienschaltung aus einem ohmschen Widerstand und einem Kondensator ein Z der Form:
Z = R - j 1/(wC) wobei w ein Maß für die Frequenz die sogenannte Kreisfrequenz ist. Es gilt w = 2*pi*f
Wie man hier sieht nimmt mit steigeneder Frequenz und steigender Kapazität der Term - j 1/(wC) ab womit auch er Scheinwiderstand immer mehr in Richtung des ohmschen Widerstandes R geht. Sprich ein Kondensator verhält sich bei hohen Frequenzen wie ein Kurzschluss und es bleibt eben nur Z = R in der Näherung über.
Wenn du nur den Scheinwiderstand der Kapazität und Induktivität betrachtest dann gilt Z = jX also für Kapaziutäten Z = -j 1/(wC) und für Induktivitäten Z = jwL. Sprich für Kapazitäten nimmt der Scheinwiderstand mit steigender Frequenz ab und für Induktivitäten nimmt der Scheinwiderstand für steigenden Frequenzen zu.
Wenn du jetzt eine Reihenschaltung aus Kondensator, Induktivität und einem ohmschen Widerstand hast gilt:
Z = R + jwL - j 1/(wC) = R + j(wL - 1/(wC))
Den Term in der Klammer kann man jetzt zusammenfassen zu w²LC/(wC) - 1/(wC) = (w²LC - 1)/(wC). Dieser Term wird also zu wenn gilt w²LC - 1 = 0 also bei w² = 1/(LC) => wR = 1/sqrt(LC)
Diese Formel bezeichnet man jetzt als Thomson Formel. Es gilt als für die Serienschaltung aus R L und C, dass zunächst der Scheinwiderstand sehr hoch ist weil für niedrige Frequenzen 1/wC sehr groß ist. Irgendwann nimmt der Scheinwiderstand ab. bei w = 1/sqrt(LC) erreicht er ein Minimum und es gilt hier nur noch Z = R (sogenannte Resonanz), für steigende Frequnezen wird wL größer und damit steigt auch der Widerstand wieder an.
Das C gehört auch in den Nenner.