LC-Schwingkreis (Reihenschaltung) - Max.-Strom in Spule?
Hallo erstmal,
ich komme bei einer Physikaufgabe aus der Uni nicht weiter. Ich habe einen LC-Schwingkreis ohne Widerstand gegeben.
Es wird eine Spannung von U=10 V angelegt. Der Kondensator hat eine Kapazität von C= 1nF. Die Spule (Induktivität) ist 30 cm lang besitzt 100 Windungen und einen Durchmesser von 2cm. Zusätzlich ist die magnetische Feldkonstante (4Pi10^(-7) N/(A^2)) gegeben. Ich habe bereits die Induktivität ausgerechnet. Nun ist die Frage welcher Maximalstrom durch die Spule fließen kann.
Mir fällt hierbei nur die Formel U= RI => I=U/R ein.
Da kein Widerstand gegeben ist, komme ich nicht weiter. Ich habe bereits nachgeschaut ob denn durch den Kondensator und die Spule ein Widerstand entsteht. Aber wenn ich es richtig verstanden habe, heben sich beide auf.
Irgendwie finde ich es nirgendwo gut erklärt. Ich wäre sehr Dankbar wenn mir jemand den Lösungsweg oder einen Lösungsansatz geben könnte.
MfG. Random ;)
3 Antworten
Die Frage dabei ist allderings mit welcher Frequenz dieser Schwingkreis angeregt wird.
Bei Resonanz heben sich dann beide gegenseitig auf und der LC Schwingkreis stellt einen idealen Kurzschluss dar.
Wenn die 10V einfach nur so am Schwingkreis anliegen passiert gar nix, weil der Kondensator keinen Strom leitet. Wenn die Frequenz sehr hoch ist sperrt hingegen die Spule.
Wenn der Schwingkreis im Prinzip aus einen auf 10V geladenen Kondensator besteht welcher an eine Induktivität gehängt wird und anschließend frei schwingt, kannst du das ganze über die Energie in der Spule berechnen.
Die Energie im Kondensator ist ja:
Ec = U²*C/2
Die Energie in der Spule Es = I²*L/2
Der maximalstrom fließt wenn der Kondensator ungeladen ist, aus der Energieerhaltung folgt dann:
Es = Ec
U²*C/2 = I²*L/2
das ganze nach I umgeformt ergibt die Formel:
I² = U²*C/L
I = U*sqrt(C/L) was dann der Formel von habakuk63 entspricht. Wichtig dabei ist nur dass hier der Schwingkreis frei schwingen muss, sobald eine Spannungsquelle am Schwingkreis hängt gilt diese Formel nicht mehr, denn dann handelt es sich um eine erzwungene Schwingung und keine Harmonische Schwingung mehr.
Stimmt ohne Dämpfung schwingt es das habe ich übersehen. Das ganze ist hald nur um den Betrag der externen Spannung nach oben verschoben.
Ich hätte anfangs gedacht, dass das Netzteil die Schwingung dämpfen würde, sofern das aber Ideal ist (Also kein Innnenwiderstand) folgt aus dem Superpositionsprinzip die Schwingung.
Wichtig für diesen Vorgang ist aber das Einschalten der Spannung, wenn die Spannung schon immer am Schwingkreis anliegt und es keinen Einschaltzeitpunkt gibt, wird allerdings keine Schwingung angeregt.
Stelle die Differentialgleichung auf. Du stellst dann fest, dass die Lösung für Uc und I harmonische Schwingung sein wird. Uc ist um einen konstanten Betrag 10V verschoben. Das muss man nicht raten (obwohl man es könnte) sondern folgt aus den Anfangsbedingen.
Diese Formel hilft, aber Umax ist nicht 10V sondern 10V * Wurzel 2
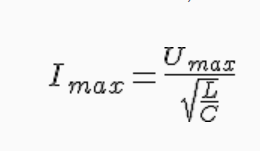
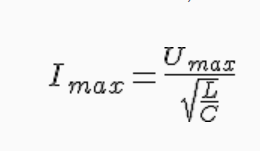
Ich glaube diese Formel stimmt. Der Schaltkreis ist glaube ich ein elektromagnetischer Schwingkreis. Dieser schwingt doch harmonisch oder ?
Naja es darf eben keine erzwungene Schwingung sein.
Sobald da irgendwo am Schwingkreis ein Frequenzgenerator drann ist, dann ist die Schwingung erzwungen.
Sofern, die Maximalspannung bzw der Maximalstrom im Schwingkreis erhalten bleiben, sollte diese Formel auch passen. Sie gilt also auch für LC Oszillatoren wo die Beschaltung quasi nur die Verluste im Schwingkreis selbst kompensiert, aber nicht mehr Energie ins System einbringt.
Bei dieser Formel muss man etwas aufpassen und ich bin mir nicht ganz sicher ob sie zur Aufgabenstelltung des TEs passt:
Diese Formel gilt nur wenn der Schwingkreis harmonisch schwingt.
Die Formel wird aus der Energieerhaltung im Schwingkreis hergeleitet (siehe meine Antwort) sobald der Schwingkreis Energie mit einem anderen System austauscht, was eigentlich immer bei externen Anregung der Fall ist gilt diese Formel nicht mehr.
Wenn die Spannung eingeschaltet wird schwingt es. Da wir hier keine Dämpfung haben, tut es das unendlich lange.