Wasserstoffatome im Grundzustand zur Emission anregen?

Aufgabe:

Können Wasserstoffatome im Grundzustand durch Wechselwirkung zum einen mit Photonen, zum anderen mit Elektronen jeweils der Energie 11 eV zur Emission von Strahlung angeregt werden? Begründe deine Antwort und berechne gegebenenfalls die Wellenlänge der emittierten Strahlung. 

Lösung:

Photonen mit 11 eV können keine Wasserstoffatome anregen, weil sie ihre ganze Energie abgeben müssten. Elektronen können das schon, sie geben dann nur 10,2 eV Energie ab und heben das Wasserstoffatom in den ersten angeregten Zustand. Beim Zurückfallen in den Grundzustand emittieren die Atome dann wieder die 10,2 eV.

Rechnung:

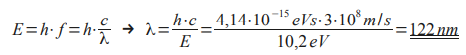
Wie kommt man darauf, dass Elektronen 10,2 eV an Energie abgeben können? Außerdem warum geben Photonen ihre Energie komplett ab? Und woher weiß man, dass Elektronen in der Lage sind, dass Wasserstoffatom in den ersten angeregten Zustand anregen können?

Danke voraus :)

Answer 1

[DrNumerus]

Wie kommt man darauf, dass Elektronen 10,2 eV an Energie abgeben können?

Beim Zusammenstoß mit anderer Materie können sie beliebig viel Energie übetragen (solange ihnen diese Energie zur Verfügung steht natürlich. Demnach können sie insbesondere auch die 10,2 eV abgeben, die zum Anregen des Wasserstoffatoms benötigt wird und werden dies auch bevorzugt tun, da das Wasserstoffatom nur genau diese Menge absorbieren kann.

Außerdem warum geben Photonen ihre Energie komplett ab?

Dieses Argument verstehe ich tatsächlich in der Lösung nicht. Ein Photon kann auch ähnlich wie ein anderes Elektron einen "inelastischen" Stoß mit einem Elektron aus dem Wasserstoffatom ausführen. Das nennt sich dann Compton-Effekt. Eigentlich sollte also ein Photon auch in der Lage sein, das Wasserstoffatom anzuregen.

Und woher weiß man, dass Elektronen in der Lage sind, dass Wasserstoffatom in den ersten angeregten Zustand anregen können?

Du kennst vielleicht die Formel für die Energieniveaus von Wasserstoff:

$E_n=-\frac{R_{\rm y}}{n^2}=-\frac{13,6\,\mathrm{eV}}{n^2}$

Wenn du also den ersten (Grund-)Zustand minus den ersten angeregten Zustand rechnest, kommst du auf:

$\Delta E=-13,6\cdot(1-\frac{1}{2^2})\,\mathrm{eV}=-10,2\,\mathrm{eV}$

Da die Aufgabe dir jetzt vorgibt, dass das potentielle Photon bzw. Elektron eine Energie von 11eV haben soll, weiß man ja, dass sie also genug Energie haben um das Atom anzuregen.

Comments

[chemieistgut]

Gut erklärt, allerdings hätte ich noch ein paar weitere Fragen :)

1. Wenn davon die Rede ist, das Wasserstoffatom anzuregen, meint man wirklich das Atom oder eher das Elektron? Wie genau kann man sich den angeregten Zustand vom Wasserstoff vorstellen? Ist ja nicht das gleiche wie bei Elektronen oder verwechsle ich da was?
2. Du hast ja 13,6 eV benutzt, die Ionisierungsenergie. Aber warum? Müsste laut der Berechnung nicht die Rydbergfrequenz benutzt werden? Also da oben bei:

-(Ry/n^2)

Wenn du also den ersten (Grund-)Zustand minus den ersten angeregten Zustand rechnest, kommst du auf:

1. Warum ist vom ersten angeregten Zustand die Rede? Könnte es nicht auch jede andere sein?

Das wäre sehr nett, wenn du das auch so gut erklären könntest :)

[DrNumerus]

@chemieistgut

Hi,

Wenn davon die Rede ist, das Wasserstoffatom anzuregen, meint man wirklich das Atom oder eher das Elektron?

Da ist tatsächlich das Elektron gemeint. Der erste angeregte Zustand bedeutet hier, dass das äußere Elektron vom Wasserstoff eine "Schale" höher liegt als das eigentlich der Fall sein sollte.

Du hast ja 13,6 eV benutzt, die Ionisierungsenergie. Aber warum? Müsste laut der Berechnung nicht die Rydbergfrequenz benutzt werden?

*Die Rydbergenergie und ja, genau das ist die Rydbergenergie... in Elektronenvolt. Das ist ja aber auch genau die erste Ionisierungsenergie, da es die Energie ist, mit dem das Elektron am Atom gebunden wird.

Warum ist vom ersten angeregten Zustand die Rede? Könnte es nicht auch jede andere sein?

Auf jeden Fall! Es kann jeglicher angeregter Zustand erreicht werden, aber in deiner Aufgabe war ja gefragt, ob die Photonen bzw. Elektronen irgendwie in der Lage sind, das Atom anzuregen. Würde man bis in den zweiten angeregten Zustand springen wollen, bräuchte man in meiner Rechnung für den Energieunterschied oben eine 3, statt eine 2 im Nenner und würde dann auf 12,08eV kommen. Das schaffen die 11eV Teilchen dann also nicht mehr ;)

Und danke für den Stern!

[chemieistgut]

@DrNumerus

Ich danke dir :)

Ich lobe jeden der sich Mühe gibt immer mit einem Stern, vor allem dann, wenn es hilfreich ist :)

Answer 2

[Wechselfreund]

Photonen "sind nach der Anregung weg", müssen also von der Energie her genau passe. Elektronen können einen Teil der Energie nach der Anregung behalten. Bei ihnen muss die Energie also mindestens der Anregungsenergie entsprechen.

Comments

[chemieistgut]

Danke, aber noch ein paar weitere Fragen:

1. Wenn das Wasserstoffatom dann zurück emittiert, werden dann wieder Photonen frei? Also ist das der gleiche Vorgang wie bei Elektronenanregung? Und wieviel werden frei? Eins oder mehr?
2. Wie kommt man jetzt auf diese 10,2 eV ?

[Wechselfreund]

@chemieistgut

Schau dir evtl. dies mal an

http://www.chemgapedia.de/vsengine/vlu/vsc/de/ch/11/aac/vorlesung/kap_2/vlu/bohrsche_atommodell.vlu/Page/vsc/de/ch/11/aac/vorlesung/kap_2/kap2_6/kap26_7.vscml.html

Aus dem ersten angeregten Zustand muss es ein Photon sein, ansonsten geht es auch mit stufenweisem Rücksprung

[chemieistgut]

@Wechselfreund

Hab ich schon... hat mir jetzt nicht sonderlich geholfen :(