Was ist der Unterschied beim Taschenrechner zwischen tan und tan^{-1}?
Wenn man mit tan^{-1} rechnet, dann kommt eine größere Zahl als bei tan, wann benutzt man welches?
6 Antworten
Oft hat man folgende Gleichung gegeben:
tan(x) = Gegenkathete / Ankathete = y
Um nun den Winkel x auszurechnen, benötigt man die Umkehrfunktion:
x = atan(y)
Bei der Umkehrfunktion von tan(x) - genannt Arkustangens - gibt es 4 Schreibweisen: arctan(x) = atan(x) = tanˉ¹(x) = tan^(-1)(x)
Nicht verwechseln mit dem Kehrwert der Funktion tan(x): 1/tan(x) = tan(x)ˉ¹ = tan(x)^(-1)
Unter http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
gibt es sehr viele Funktionen und ihre Umkehrfunktionen.
Beachte: den Winkel kann man neben der normalen Basiseinheit "rad"
auch in der veralteten Einheit ° (Grad; Taschenrechner DEG) angeben:
rechter Winkel = Pi/2 [rad] = 90°
Mit „tan⁻¹“ ist die Umkehrfunktion von „tan“ gemeint.
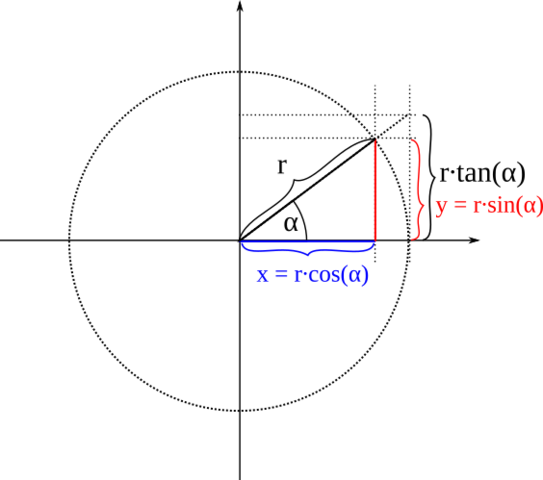
Im Bild ist ein rechtwinkliges Dreieck mit den Katheten x und y und der Hypotenuse
r = √{x² + y²}
dargestellt. Wenn Du den Winkel α kennst und das Verhältnis
y/x = tan(α)
wissen willst, musst Du „tan“ benutzen, wenn Du y/x kennst und α ausrechnen willst, „tan⁻¹“.
Zusatzinformation zur Schreibweise
Die Bezeichnung ist etwas irreführend, denn in Anlehnung an
sin²(α) := (sin(α))²
könnte „tan⁻¹“ auch als
(tan(α))⁻¹ = 1/(tan(α))
missverstanden werden; das ist aber der Cotangens und wird mit „cot(α)“ oder der aus naheliegenden Gründen bevorzugten Schweibweise „ctg(α)“ bezeichnet.
Mit „tan⁻¹“ ist hingegen die Umkehrfunktion der Tangensfunktion gemeint, der Arcustangens-Funktion, die mit „arctan(α)“ oder „atan(α)“ bezeichnet wird.
Der Bezeichnung „tan⁻¹“ liegt eine etwas abstrakte Vorstellung zugrunde, die „tan“ als Operator auffasst, der mit dem Winkel α gleichsam multipliziert wird und dabei dessen Tangens ausspuckt. In diesem Sinne wird der Arcustangens-Operator als eine Art „Kehrwert“ des Tanens-Operators aufgefasst.
Die „Eins“ im Reich der Operatoren ist der Identitätsoperator „id“, der eine Größe auf sich selbst abbildet: id(α)=tan⁻¹tanα = α.
Das gilt natürlich nur in einem begrenzten Bereich von α.
Nachtrag:
…dann kommt eine größere Zahl als bei tan…
kann nur sein, wenn der Rechner auf DEG eingestellt ist. Wenn arctan(y/x) im Bogenmaß ausgegeben wird, kommt immer etwas Kleineres heraus.
tan(α)=Gegenkathete/Ankathete. α=tan^-1(Gegenkathete/Ankathete)
Den normalen tangens benutzt du,um mithilfe eines Winkels und einer Seite eine zweite Seite zu berechnen. Den tangens -1 kannst du benutzen,um mithilfe von zwei Seiten einen Winkel auszurechnen,also genau umgekehrt.
wie muss ich das eingeben, wenn ich zum beispiel die zweite seite berechnen will? also tan und dann winkel und dann in klammern die seite oder wie genau?
tan ist Tangens und tan^-1 ist arcustangens also praktisch der Tangens bloß umgedreht