Was genau ist das Skalarprodukt?
Was genau ist das Skalarprodukt bei der Vektorrechnung konkret? Ich weiß, wenn das Skalarprodukt =0 ist, hat man eine Orthogonale nachgewiesen. Aber was für ein Skalar wird berechnet? Was sagt z.B. eine =21 aus, außer, dass keine Orthogonale besteht?
Danke im Voraus!
4 Antworten
Das skalare Produkt zweier Vektoren ist gleich dem Produkt des Betrages des ersten Vektors und der Länge der vektoriellen Projektion des zweiten auf den ersten Vektor (also der Länge der roten Linie auf dem Bild von Monsiedekay)
ACHTUNG: Das skalare Produkt ist nicht die Länge der roten Linie!!!
Nimm dir ein kariertes Blatt und zeichne die Vektoren (5,0) und (3,4) ein, beide vom selben Punkt ausgehend → das skalare Produkt errechnet sich aus Produkt der x-Koordinaten vermehrt um das Produkt der y-Koordinaten - hier also 5·3+0·4=15.
Die Projektion auf den Vektor (5,0) - also die rote Linie - beträgt aber nur 3
hier noch mal ein Foto zur Veranschaulichung. Die Länge der roten Linie ist das Skalarprodukt von v1 und v2.... wenn die beiden senkrecht zueinander stehen, wäre die Länge dann logischerweise 0
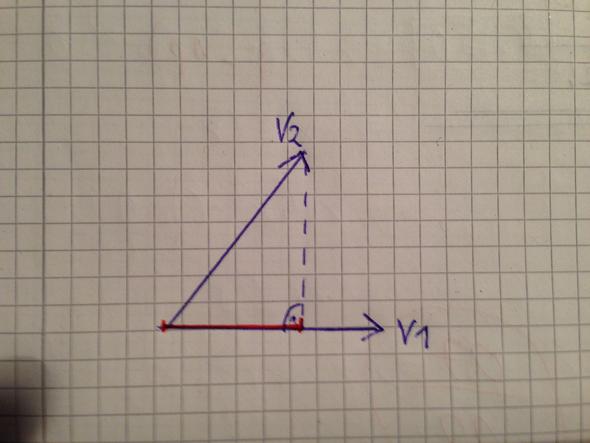
kleine Ergänzung noch... wenn die Projektion von v2 in die entgegengesetzte Richtung von v1 gehen würde (also wenn v2 auf dem Foto z.B. nach Nord-West zeigen würde), wäre das Skalarprodukt negativ
Das ist falsch! Die Länge der roten Linie ist nicht das skalare Produkt der beiden Vektoren!
Aber zur Veranschaulichung der Projektion ist das Bild sehr gut :-)
das skalarprodukt zweier vektoren ist die projektion des einen vektors auf den anderen.
wenn beide vektoren orthogonal sind, dann ist die projektion logischerweise 0.
gruß
das Skalarprodukt gibt die Länge an, wenn ein Vektor auf einen anderen projeziert wird (Pfeilspitze wandert senkrecht auf den ersten Vektor)