Wieso sind zwei Vektoren Orthogonal, wenn das Skalarprodukt 0 beträgt?
3 Antworten
Allgemein gilt im zwei- und dreidimensionalen Raum:
<a,b> = |a| * |b| * cos(φ), wobei <a,b> das Skalarprodukt ist, |.| die Länge der Vektoren bezeichnet und φ der Winkel zwischen a und b ist.
Algebraisch ist klar, dass hier 0 rauskommt, wenn φ=90° gilt, denn cos(90°)=0.
_____
Es gibt aber auch eine geometrische Erklärung:
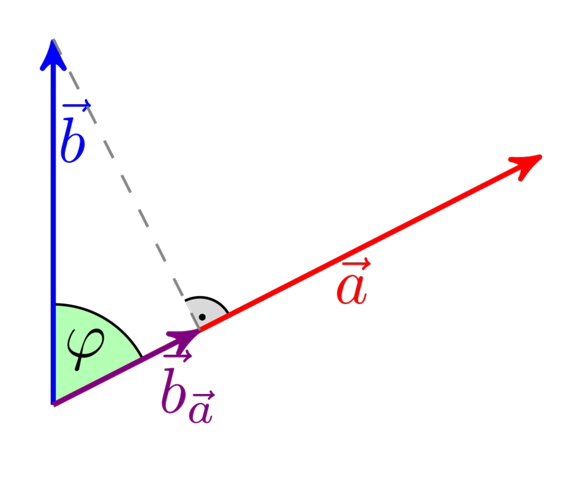
Man kann laut der folgenden Zeichnung den Teil mit |b|*cos(φ) durch b_a ersetzen, denn es gilt: cos(φ)= b_a / |b|

Also folgt <a,b>=|a|*b_a.
Wenn jetzt a senkrecht auf b steht, ist b_a offenbar 0 und man hat <a,b>=|a|*0, oder <a,b>=0.
siehe Physik-Formelbuch,was man privat in jedem Buchladen bekommt.
Defintion:Arbeit W ist das Produkt aus der Kraft F mal längs des Weges s
W=F*s
F und s sind Vektoren,die zu jeder Zeit parallel zueinander liegen,sonst gilt die Formel nicht
W ist eine Zahl,ein Skalar
Daher kommt der Ausdruck Skalarprodukt
Steht nun F senkrecht auf s,so ist die Arbeit W=0 also das Skalarprodukt gleich NULL
im 3 dimensionalen Raum
Skalarprodukt
a*b=ax*bx+ay*by+az*bz=0 wenn die beiden Vektoren a(ax/ay/az) und b(bx/by/bz) senkrecht aufeinander stehen.
Weil der cosinus von 90 Grad = 0 ist, siehe
https://de.wikipedia.org/wiki/Skalarprodukt