Warum wählt man beim Heron-Verfahren immer den Mittelwert?

Gute Frage, man könnte statt der Iteration

x(n+1) = (x(n) + a/x(n)) / 2

genauso gut mit

x(n+1) = (x(n) + 2*a/x(n)) / 3

arbeiten. Im ersten Fall wird der Mittelwert (x(n) + y(n)) / 2 als neue Seitenlänge des Quadrats mit Fläche a genommen, im zweiten Fall (als Beispiel von mir) der gewichtete Mittelwert (x(n) + 2y(n)) / 3. Die Formel ist halt etwas komplizierter und die Konvergenz ist nicht so schnell.

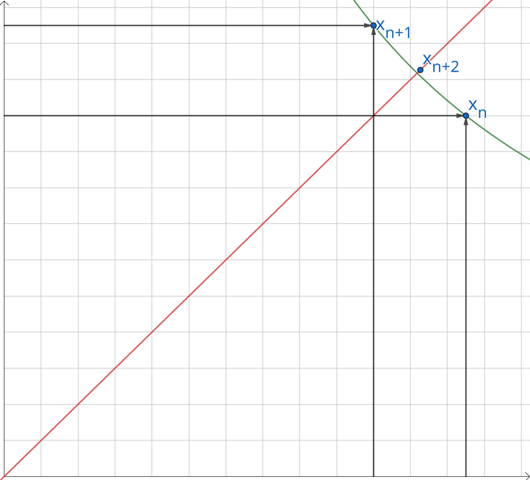
Das ist ganz anschaulich: Du hast die grüne Funktion y=N/x und suchst deren Fixpunkt (=Schnitt mit der roten Diagonalen):

⠀⠀⠀⠀

In jeder Iteration hast Du eine Näherung xₙ und xₙ₊₁=N/xₙ. Die schwarzen Rechtecke haben beide die Fläche N. Der Fixpunkt liegt knapp unter der Mitte von xₙ und xₙ₊₁. Tatsächlich ist der Fixpunkt das geometrische Mittel aus xₙ und xₙ₊₁. Wenn Du das berechnen kannst, brauchst Du das Heronverfahren gar nicht. Ansonsten ist das arithmetische Mittel hier als Näherung xₙ₊₂ recht „naheliegend“, denn die grüne Kurve hat im Fixpunkt die Steigung −1.

Weder Herr Heron noch ich haben eine Idee, wie man mit einfachen Mitteln eine noch bessere Näherung xₙ₊₂ bestimmen könnte. „Mit einfachen Mitteln“ heißt: weniger Rechenaufwand und eine bessere Näherung als k Heron-Schritte.

Anfangs weicht das arithmetische Mittel zwar noch deutlich vom geometrischen ab, aber das Verfahren konvergiert so schnell, dass sich eine Optimierung auch da nicht lohnt.

Die Lösung muss ja zwischen der langen und der kurzen Seite liegen. Wenn man den Mittelwert nimmt, konvergiert die Berechnung zum einen schnell, zum andern ist damit der Algorithmus einfach.