Wann kommt aus der Wurzel eine natürliche Zahl heraus?
Für welche ganzzahligen Werte von a und b kommt aus der unterstehenden Wurzel eine natürliche Zahl heraus?
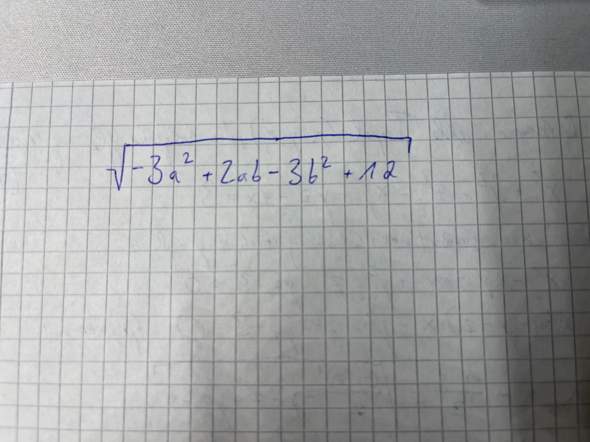
3 Antworten
Ich würde zuerst die 2. Binomische Formel anwenden, um den Ausdruck unter der Wurzel zu
12-(a-b)^2-2a^2-2b^2
Da die Wurzel nur definiert ist, wenn der Term in der Wurzel nicht negativ ist, musst du dich nur auf die a und b beschränken, wo (a-b)^2+2a^2+2b^2<12 gilt. Da gibt es nicht allzu viele Fälle.
Das weiß ich. Aber da steht doch eine -3 vor dem a^2 und b^2…
Du hast a^2 -3 Mal . Du "klaust" eins davon und nutzt es für die binomische Formel.
Du kannst es auch einfach umschreiben:
-3a^2+2ab-3b^2 = -2a^2-2b^2-(a^2-2ab+b^2)
Macht es das etwas deutlicher?
Und dann kann man sich noch überlegen, welche Quadratzahlen kleiner 12 ist gibt, dann hat man noch weniger Fälle...
Unter der Wurzel steht
-2a^2 -(a-b)^2 -2b^2 + 12
Das darf zumindest nicht negativ sein, also sind a und b auf die Werte -2, -1, 0, 1 und 2 beschränkt. Beide dürfen sich auch nicht um mehr als 3 unterscheiden. Die paar Möglichkeiten durchzuprobieren überlasse ich dir.
Vielen Dank für die Antwort! Wie kommst du auf den Bereich von -2 bis 2 und warum dürfen sie sich nicht um mehr als drei unterscheiden?
Da gibt es nicht sooo viele Möglichkeiten.
a=0, b=1
a=1, b=0
a=0, b=-1
a=-1, b= 0
Da ist das Ergebnis der Wurzel gerade 3.
a = 0, b=2
a = 2, b=0
a=0, b= -2
a= -2, b= 0
Da ist das Ergebnis der Wurzel gerade 1.
Da ist das Ergebnis der Wurzel 0 (und in der Regel zählt die Null als natürliche Zahl)
a = 1, b = 2
a = 2, b = 1
a = -1, b=-2
a= -2, b= -1
Es lässt sich verhältnismäßig einfach zeigen, dass das alle Lösungen sind.
Wofür brauchst du das?
Schreib es einfach sauber auf.
kann nur dann eine natürliche Zahl sein, wenn der Ausdruck unter der Wurzel größer oder gleich 0 ist.
Du hast dann also
Das kannst du umformen zu
was wiederum dasselbe ist wie
Da siehst du in der Mitte die binomische Formel, und bekommst
Jeder Summand links ist größer oder gleich Null, soll aber in der Summe kleiner gleich 12 sein, damit bekommst du schnell obere Grenzen für die beiden Werte für a und b.
War eine Knobelaufgabe aus dem Matheunterricht. Aber wie lässt sich zeigen, dass es keine anderen Lösungen mehr geben kann?
Ich hab es in meiner Antwort noch mal erläutert, da geht das mit dem Formelsatz besser.
Danke! Aber wie kommst du auf die zweite Binomische Formel? Die kann ich irgendwie nicht erkennen.