Umkehrfunktion von einem Teilintervall einer Funktion berechnen?
Hi, wenn ich eine Funktion habe z.B. f(x) = x^2 + 2x - 15, dann kann man von dieser Funktion keine Umkehrfunktion berechnen, da sie nicht streng monoton wachsend/ fallend ist. Aber wenn man nur das Intervall [-1, unendlich) betrachtet, dann ist die Funktion für dieses Intervall umkehrbar, aber wie berechne ich dann die Umkehrfunktion?
2 Antworten
Die Gleichung wird einfach mit Hilfe der p-q-Formel nach x aufgelöst und liefert die Umkehrfunktion. Nun muss man allerdings wählerisch sein bezüglich des Wurzelvorzeichens. Nur ein Vorzeichen darf gültig sein. Aber welches? Dies muss man prüfen gegen die Einschränkung, dass man nur das Intervall [-1, unendlich] umkehren will. Ein Blick auf den Graph zeigt, dass uns das positive Vorzeichen den Gefallen tut. Eine gute Orientierung bietet die Spiegelung des Funktionsgraphen (blau) an der y=x-Diagonalen als Hinweis auf den Graphen der Umkehrfunktion (rot).
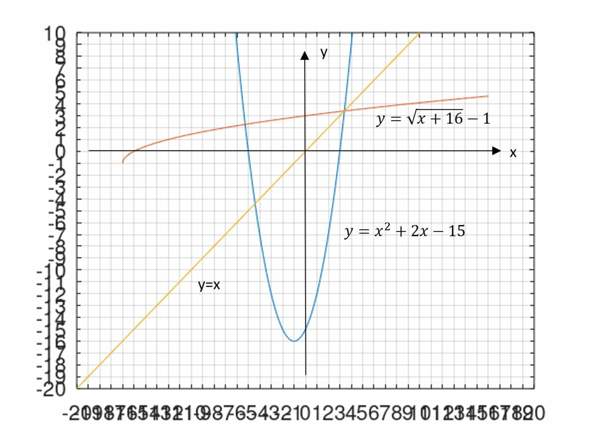
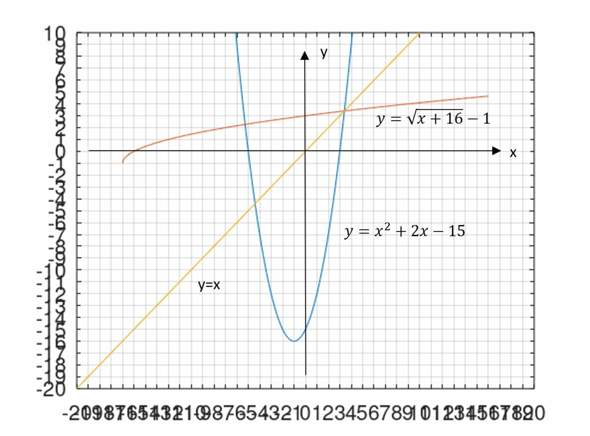
Ja, sicher komme ich auf das gleiche Ergebnis. Es steht doch in der Grafik. f-1(x) = (16+x)^0.5-1
Indem du die Gleichung
y = x^2 + 2x -15 <=> x^2 + 2x -15 - y = 0
mit Hilfe der pq-Formel nach x auf löst.
Danke, habe es mit der Mitternachtsformel gelöst. Ich war zuerst verwirrt, weil man ja (15-y) als Zahl hat und dann die Wurzel der Mitternachtsformel nicht auflösen kann, aber wenn ich f(f^-1(x)) rechne kommt tatsächlich x heraus, also müsse mein f-1 ja stimmen. Ich habe f-1(x) = (-2+ (64+4x)^0.5) / 2. Kommst du auf das gleiche Ergebnis?