Stochastik Mathe?
Wie löst man die a.)? Bitte genau erklären
2 Antworten
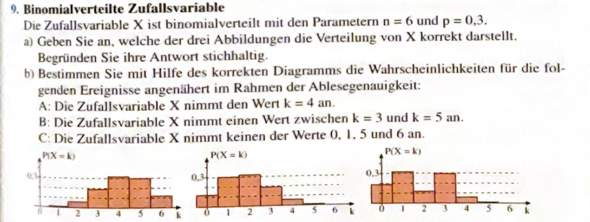
a) der Erwartungswert liegt bei n*p=6*0,3=1,8 d. h. es ist bei 6 Versuchen und einer Trefferwahrscheinlichkeit von 0,3 (=30%) eine durschnittliche Trefferzahl von 1,8 zu erwarten, und das heißt, dort muss die Wahrscheinlichkeit P(X=k) am höchsten sein.
Und von dort fallen die Wahrscheinlichkeiten nach links und rechts kontinuierlich ab. Somit kommt nur das mittlere Diagramm in Frage; links ist die Wahrscheinlichkeit bei k=4 am höchsten und rechts geht es rauf und runter, d. h. dieses Diagramm fällt von vornherein schon raus, egal wie groß n und p sind.
Hier ist mit "zwischen k=3 und k=5" sicher gemeint, dass k=3 und k=5 dazu gehören - wortwörtlich genommen liegt ja nur die 4 zwischen 3 und 5...
D. h. hier ist nach P(3<=X<=5) gefragt, also nach P(X=3)+P(X=4)+P(X=5)=0,2+0,07+0,01=... (wobei man die hinteren beiden Wahrscheinlichkeiten nicht genau ablesen kann).
Wie geschrieben, kann man die exakten Wahrscheinlichkeiten nicht ablesen - daher würde ich auf die Tausendstelstelle (=3. Nachkommastelle) verzichten.
Gehe ich von "meinen" Ablesewerten aus, dann ergibt das 0,2+0,07+0,01=0,28.
Siehst Du bei k=4 eher 0,05 steht 0,07, dann kommst Du auf p=0,2+0,05+0,01=0,26.
Aber rein rechnerisch kommt tatsächlich 0,255 raus!
Hallo,
das mittlere Diagramm paßt.
Du brauchst doch nur die Wahrscheinlichkeit für k=0 berechnen, dann siehst Du schon, welches das Richtige ist. Mit k=1 bis 6 kannst Du das Ergebnis noch absichern.
Die Wahrscheinlichkeit für ein bestimmtes k berechnest Du nach der Bernoulliformel:
P(x=k)=(n über k)*p^k*(1-p)^(n-k).
Herzliche Grüße,
Willy
Warum nicht? Bei k=0 unterscheiden sich die drei Diagramme ganz gut.
Und was rechnet man bei B: von der b)