Stammfunktion bezüglich spezieller Punkte im Graphen Hilfe?
Guten Tag,
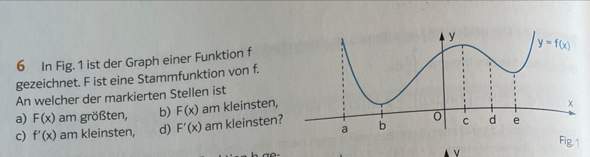
Ich bin bei einer Mathematikaufgabe, bei der ich nicht weiterkomme. Dabei ist ein Graph gegeben. Nun muss angegeben werden, bei welchem Punkt die Funktionen am größten/kleinsten sind. Danke für Hilfe, LG
2 Antworten
a) f(x) ist die Ableitung von F(x). Und f liegt ausnahmslos über der x-Achse, d. h. die Steigung von F ist durchweg positiv. Und d. h. die Funktionswerte von F steigen immer weiter an...
b) ergibt sich aus der Beschreibung unter a)
c) f' ist die Steigung von f, d. h. dort, wo der abgebildete Graph am stärksten fällt ist f' am kleinsten
d) der abgebildete Graph von f(x) ist zugleich der Graph von F'(x)
Tipp: F'(x) = f(x)
Wenn es klar wäre, ergäben sich die Antworten. In der anderen Antwort hat sich ja eine mitleidige Seele gefunden.
Damit der Kopf am Wochenende frei ist für andere Dinge! :)
Das ist falsch. Nur weil ich weiß, was die Ableitung der Stammfunktion ist, heißt es nicht, dass automatisch über die graphischen Charakteristika Kenntnis verfügt wird. Wenn ich wissen würde, wie die Stammfunktion aussehen würde, dann ergäbe es sich von selbst. Wenn ich allerdings nur weiß, dass die Ableitung der Stammfunktion die Originalfunktion ist, dann kann ich keine Rückschlüsse mit Spezifikation ziehen, es sei denn ich verfüge Kenntnis über das graphische Aussehen. Die „mitleidige Seele“ wie Du sie nennst, hat eine richtige Antwort geliefert, wovon in einem Frageportal auszugehen ist. Nichtsdestotrotz ist das nicht böse gemeint.
Ok, ich war wohl (fälschlicherweiser) davon ausgegeangen, dass durch meinen Tipp klar wird, dass der abgebildete Graph den Steigungsverlauf der Stammfunktion darstellt, da die Ableitung einer Funktion ja deren Steigung angibt.
Also a) e
b) a
c) a
d) b