Rang einer Matrix bestimmen?
Kann mir vielleicht jemand sagen wie man es machen muss bitte
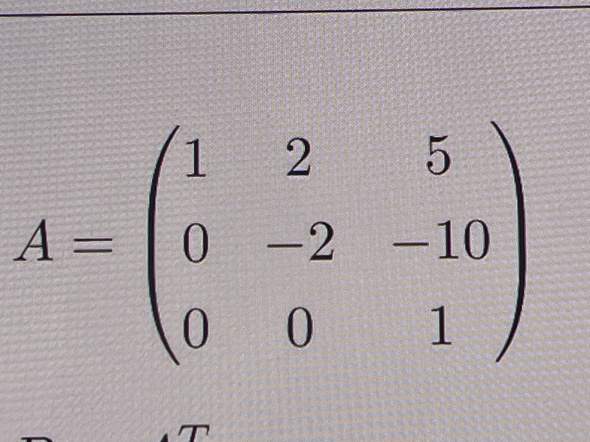
3 Antworten
Kannst Du ablesen, da die vorliegende Matrix schon in Zeilenstufenform vorliegt ist der Rang dieser Matrix gleich 3, also Rang(A)=3
Andernfalls müsstest Du die Matrix in Zeilenstufenform bringen (z.B. mit dem Gauß-Verfahren) und dann die Zahl der Zeilen ablesen, die ungleich 0 sind.
Siehe auch: https://www.mathebibel.de/rang-einer-matrix
An der Dreiecksform kann man erkennen, dass die Determinante der Matrix 1*(-2)*1 = -2, also von Null verschieden ist. Die Matrix ist somit invertierbar und hat vollen Rang 3.
Das reicht hier aber - ich mache mir das Leben nicht unnötig schwer, wenn es nicht notwendig ist. Zudem kann man in Fällen, in denen die Determinante 0 ist, immer noch Rangbetrachtungen durchführen…
immer noch Rangbetrachtungen
Genau dabei wollte der FS Hilfe ...
Auch ohne Determinante sieht man, dass es keine Nullzeile gibt, der Rang also 3 ist.
Auch ohne Nullzeile kann eine Matrix singulär sein, nicht jedoch bei nicht-verschwindender Determinante…
Wenn ich richtig lesen kann, fragt der Fragesteller, wie man den Rang einer Matrix bestimmt --> Man überführt in Stufenform und zählt die Nicht-Null-Zeilen
Auch ohne Nullzeile kann eine Matrix singulär sein
Nachdem die Stufenform hergestellt wurde? Dafür hast du sicher ein Beispiel. Man lernt ja immer gern dazu.
Nein, dann nicht - aber dafür muss man erstmal die Stufenform herstellen; bei niederdimensionalen Matrizen ist die Berechnung der Determinante viel einfacher als Zeilen und Spaltenumformungen durchzuführen…
Oder die Stufenform liegt - wie in diesem Beispiel - bereits vor ...
Um einen nicht-vollen Rang zu bestimmen, kommt man um die Stufenform wohl nicht herum. Zumindest nicht mit Schülerwissen.
Mir war nicht klar, dass in der Schule überhaupt mit Matrizen gerechnet wird bzw. der Rang einer Matrix bestimmt wird. Ich habe davon erst im Mathematikstudium gehört…
Sogar im Grundkurs. Abschnitt Lineare Algebra. Wenn es um die Anzahl der Lösungen linearer Gleichungssysteme geht.
LA haben wir in der Schule nicht gemacht, dafür aber Analytische Geometrie und Analysis mit DGLs; aber egal…
Wenn du die Matrix mit dem Gauß-Verfahren soweit möglich in Treppenform bringst, dann gibt die Anzahl der Zeilen ungleich Null den Rang der Matrix an. Hier ist es offenbar 3.
Mit dem Umweg über die Determinante kann man aber nur entscheiden ob voller Rang vorliegt oder nicht. Determinante = 0 sagt nicht, ob der Rang 0,1 oder 2 ist.