partielle Ableitungen?
Wie kann ich diese Funktion nach x und y ableiten? Habe es mit der Quotientenregel versucht, aber kriege sie nicht so wie in der Lösung vereinfacht.


4 Antworten
nach x ableiten
u' = y
v' = 1/2 * (x²-y +1)^(-1/2) * 2x
.
y * (x²-y +1)^(1/2) - (xy-4)*(x²-y +1)^(-1/2)*2x
im Nenner steht (x²-y+1)^1
Beim Minus aufteilen und vereinfachen zu

.
Dann den vorderen Bruch mit (x²-y+1) erweitern und die Zähler zusammenfassen
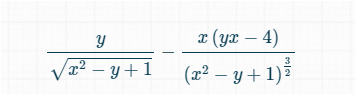
Kannst du schreiben als:
f(x, y) = (x * y - 4) * (x ^ 2 - y + 1) ^ (- 1 / 2)
Und nun kannst du ganz normal mit Produktregel und Kettenregel ableiten. Wenn du nach einer Variablen partiell ableitest, dann musst du gedanklich so tun als wäre die jeweils andere Variable nur eine Zahl.
f(x) differenziert nach x nach der Qotientenregel ergibt
(sqrt(-y+x^2+1)y-(x(xy-4)/sqrt(-y+x^2+1))/(-y+x^2+1)
Wir substituieren a=-y+x^2+1. Dies ergibt
(sqrt(a)y-(x(xy-4))/sqrt(a))/a
Wir bringen den Zähler auf einen Nenner
(ay-x(xy-4))/(sqrt(a)/a)
Wir desubstituieren a
((-y+x^2+1)y-x(xy-4))/(-y+x^2+1)^(3/2)
Wir fassen den Zähler zusammen. Dies ergibt
(-y^2+y+4x)/(-y+x^2+1)^(3/2)
Bemerkte das die hoch 3 unter der Wurzel kombiniert hoch -3/2 ergibt .
Es ist einsichtiger mit Produktregel statt quotientenregel.