Nullstellen Potenzfunktion
Hallo, ich soll die Nullstellen der Funktion f(x)= x^3 -2x^2 +x durch Ausklammern berechnen, dies habe ich getan, bekomme aber bei einem Programm das den Graph zeichnet andere Nullstellen als bei meiner Rechnung raus.
0 = x^3 -2x^2 +x /gleich Null gesetzt
0 = x (x^2 -2x +1) /x ausgeklammert
x^2 -2x +1 => p=-2; q=1 /Werte in p/q-Formel eingesetzt
meine Lösung lautet: x1 = 0; x2 = 1; x3 = 1
Kann mir bitte jemand sagen, was ich falsch mache?
5 Antworten
Du hast alles richtig gemacht und wenn man den Graphen zeichnet, kommen dieselben Nullstellen raus:
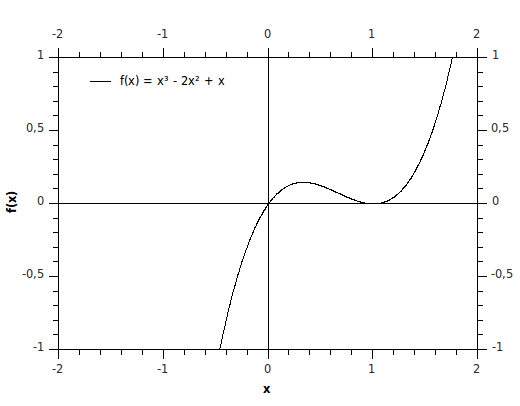
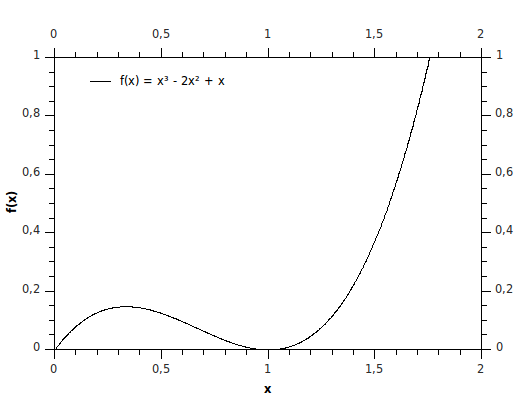
Du machst nichts falsch, das ist absolut richtig. Du musst dein Ergebnis ja nur wieder ins Polynom einsetzen, dann siehst du, dass da Null rauskommt.
Ein anderer Rechenweg ist übrigens, die binomische Formel rückwärts anzuwenden:
x (x^2-2x+1)= x (x-1)^2.
Daran ließt du gleich ab, dass 0 eine Nullstelle ist und 1 eine zweifache Nullstelle.
pq-formel x2,3 = 1±wurzel(1-1) also x2=1
Abgesehen davon, dass es keine Potenzfunktion, sondern eine ganzrationale Funktion ist, machst du nichts falsch
du hast einen Fehler bei der pq-Formel. Wahrscheinlich einen Vorzeichenfehler
-p/2 +/- ((p^2/2)-q)^0,5
2/2 +/- (-2^2/2)-1)^0,5
-p/2 +/- ((p²/2)-q)^0,5
Stimmt nicht. Richtig ist:
-p/2 +/- ((p²/4)-q)^0,5
oder eben -p/2 +/- ((p/2)²-q)^0,5
Und btw: Das sollte man bei diesen Werten auch noch ohne Taschenrechner hinkriegen^^
Und dein Onlinerechner gibt auch das Richtige aus. x = 1
dann hat jemand diesen online rechner für pq formeln falsch programmiert. Hatte leider nicht meinen eigenen Taschenrechner zur Kontrolle vor mir.
Der von dir verlinkte Rechner funktioniert (zumindest für das vorliegende Beispiel) einwandfrei. Für die vorliegende Funktion f ( x ) = x ² - 2 x + 1, also für die Werte p = - 2 und q = 1, liefert er völlig korrekterweise die einzige Nullstelle x = 1.
da ist kein Fehler, das Ergebnis ist richtig.