Minimale vom Dreieck die aus der Wendetangente gebildet wird?
Moin moin,😭
ich hätte eine Frage, also in der Aufgabe 7d zweiter Teil (siehe Bild) weiß man die Wendetangente und diese bildet mit der x- und y-Achse einen Dreieck wie bestimmt man den minimalen Flächeninhalt des Dreiecks?
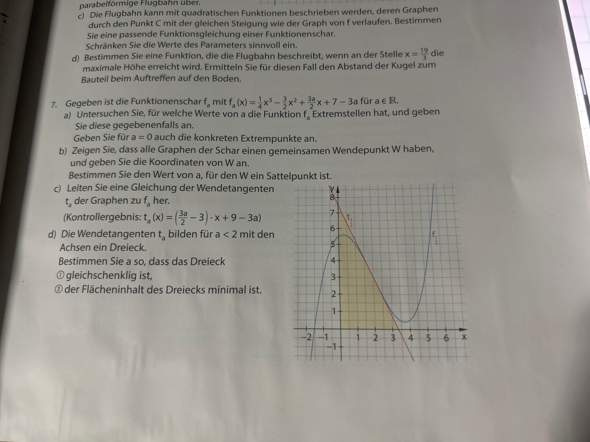
Ich bin da leider überfordert und weiß echt nicht wie ich daran soll, wir haben weder gelernt wie man eine minimale berechnet noch wie man es mit GTR löst, unsere Lehrerin hatte nur gemeint, dass man es mit GTR lösen könnte.
danke für Antworten🥰
1 Antwort
Das ihr nicht gelernt habt wie "minimale" berechnet werden kann ich mir nicht vorstellen, immerhin geht es in diesen Aufgaben bereits um Extremstellen. Und auch hier seid ihr in dem Thema nicht gerade erst am Anfang, wenn es bereits um Funktionchars und Wendepunkte geht.
Dennoch...
Wie berechnet sich denn im Allgemeinen der Flächeninhalt eines Dreiecks?
Das Dreieck (oder auch alle Dreiecke der Char), sind ja sogar rechtwinklig, was die generelle Rechnung vereinfacht.
Wenn du also weißt wie sich der Flächeninhalt eines solchen Dreiecks prinzipiell berechnet, solltest du dir überlegen, was du dann im Bezug auf diese Aufgabe für Infos brauchst und woher diese kommen (woher bedeutet hier, welche Funktionen oder Punkte)
Außerdem musst du beachten das das Dreieck auch noch gleichschenklig ist.
Gleiches Spiel. Was macht ein gleichschenkliges Dreieck aus?
LG