Der maximale Flächeninhalt einer Funktion ist gefragt (Analysis)?

Die Tangentengleichung ist y= -e^-ux +1 - 1/e, Für welches u hat das Dreieck, das aus der Tangente und den beiden Koordinatenachsen gebildet wird, maximalen Flächeninhalt ?
4 Antworten
Hallo Melinda,
ich weiß jetzt nicht ganz genau, wie du das berechnen sollst, ich habe dir aber alles vorbereitet. Zu erst solltest du dir die Tangentengleichungen aufstellen. Ich hab das mal gemacht. Die obere auf dem Zettel war nur ne Übung für mich, um selbst wieder reinzukommen.

Die beiden t(x) und die Funktion f(x) werden nun in einem Excel-Diagramm dargestellt.
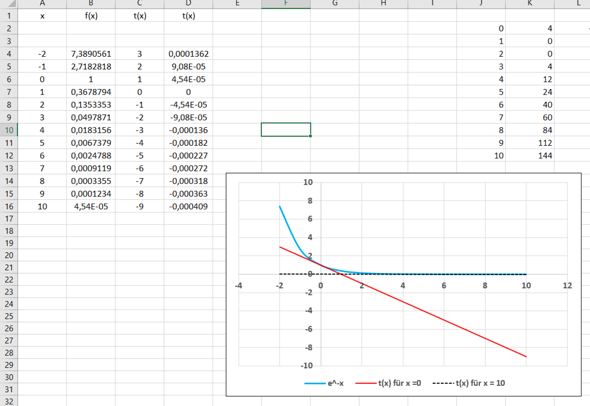
Die f(x) (blau) und die Tangenten (rot und schwarz) bilden ein kleines Dreieck, siehst du das? Und die Frage ist wahrscheinlich, dass du jetzt das Dreick, das du reinmalen könntest, ja verschieden zeichnen könntest. Aber nur für eine Höhe bekommst du den maximalen Flächeninhalt.


Wow Danke ich bin begeistert, du hast dir viel Mühe gegeben, Danke
Da wir die Tangente aus Teil a) nicht kennen kann man dazu natürlich wenig sagen. Aber generell mußt du die Dreiecksfläche in Abhängigkeit von der gewählten Tangente (also einem Parameter) ausrechnen, und das Maximum dieser Funktion ausrechnen.
Wie wäre es wenn du erstens die komplette Aufgabe hier hinein kopierst (ohne Interpretationen und "weglassen" deinerseits) und zweitens mal selbst versuchst das zu machen was ich geschrieben habe?
Diese Tangente, also die Koordinaten des Schnittpunktes usw., also die bräuchte man schon, gell...
Damit kann niemand was anfangen.
Was ist u?
Wie soll ein Dreieck entstehen, wenn zwei der drei Seiten parallel zu einander sind (x=0 x=10)?
Die Tangentengleichung ist = -e^-ux+1-1/e