Maximaler Flächeninhalt des Dreiecks?
Hallo,
Ich habe eine kurze Frage bezüglich dieser Aufgabe.
Gegeben sind die Funktionen f und g mit f(x)=-1/5x3+5x und g(x)=x im Intervall 0 kleiner, gleich x kleiner gleich √20. Der Punkt P(a|f(a)), der koordinatenursprung und der Punkt Q (a|g(a)) bilden einen Dreieck.
Für welchen Wert von a ist die Fläche des Dreiecks am größten?
Ich habe schon die Lösung, die wie folgt lautet: F(a)=1/2· (f(a)-g(a)) ·a
Ich habe verstanden warum die Grundseite g = f(a) - g(a) ist.
Kann mit aber bitte jemand erklären, warum a die Höhe ist. Weil ich das irgendwie nicht verstanden habe.
Ich würde mir sehr auf eine Antwort freuen.

3 Antworten
Die Höhe kann auch außerhalb eines Dreiecks liegen. Sie muss nur senkrecht zur Grundseite und durch den gegenüberliegenden Eckpunkt verlaufen.
Hallo,
die Senkrechte durch x=a und x=a stehen senkrecht aufeinander, so daß das Dreieck
(0|0) (a|0) (a|f(a)) ein rechtwinkliges Dreieck bilden mit der Fläche a*f(a)/2.
Davon ziehst Du das Dreieck a²/2 ab, um die zu maximierende Fläche zu bekommen.
Da sich an den Verhältnissen nichts ändert, kannst Du das Ganze auch mit 2 multiplizieren, um die 2 im Nenner loszuwerden.
Leite die Flächenfunktion F(a)=a*f(a)-a² nach a ab, setze die Ableitung gleich Null und löse nach a auf.

Herzliche Grüße,
Willy
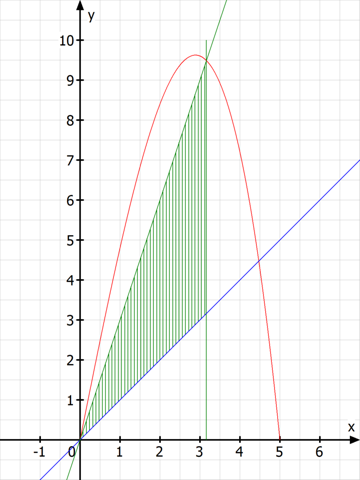
Zur Kontrolle: a=Wurzel (10), die maximale Fläche umfaßt 10 Flächeneinheiten.
Drehe einfach mal das Schaubild um 90° im Uhrzeigersinn!
--> Die Höhenlinie steht immer senkrecht zur Grundseite!
Danke für die Antwort. Die Höhenliniet scheint aber nt so groß zu sein wie a. Wie stellt es man denn fest?
Das habe ich verstanden. Aber die Höhe entspricht ja nicht die Gerade vom Ursprung zur X - Koordinate a. Wäre es ein rechtwinkliges Dreieck gilt es so, aber das ist nicht rechtwinklig. Die Höhe geht vom Ursprung diagonal zu einem Punkt auf der Grundlinie!
Danke für die Antwort. Ich frage wegen des Dreiecks in Grau unf nicht den Weißen.