Mathematik: Kehrwert einer Bruchgleichung mit Summe oder Differenz?

$Funktion\ nach\ G\ umstellen:\ Y=\ \frac{1}{1-c_1}\cdot G\ |\left(\ \right)^{-1}$ $hierzu\ Kehrwerte\ von\ \Pr odukt\ und\ von\ Quotient\ bilden:$ $\Leftrightarrow\ \frac{1}{Y}=\left(1-c_1\right)\cdot\frac{1}{G}\ |\cdot G\ |\cdot Y$ $Ergebnis:\ \Rightarrow\ G=\left(1-c_1\right)\cdot Y\ \Leftrightarrow\ G=Y-c_1\cdot Y$

Wie lauten aber die Zwischenschritte zur Bildung eines Kehrwerts bei einer Bruchgleichung mit Summe oder Differenz? Vielen Dank im Voraus.

$bei\ Summe:\ a=\frac{b+c}{d+e}\ \Rightarrow\ b=?$ (hier bitte mit dem Kehrwert arbeiten und nicht |* d+e im nächsten Schritt rechnen)

$bei\ Differenz:\ \frac{1}{g}=\frac{1}{f}-\frac{1}{b}\ \Leftrightarrow\ g=\frac{f\cdot b}{b-f}$

Answer 1

[Halbrecht]

wird eine Glg mit der Operation "Kehrwert" behandelt , muss man jede Seite komplett so ummodeln.

daher gilt bei deiner <<<Differenz>>> dieses

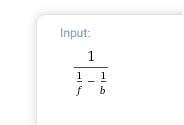
und wird nach umformung ( Nenner gleichnamig machen und den Kehrwert im Nenner mit dem Zähler verschmelzen ) hierzu

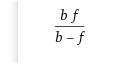
1/ ( 1 * b /f*b - 1 * f / fb ) = 1 / ( ( b - f ) / fb ) = fb / ( b - f )

https://www.wolframalpha.com/input/?i=1%2F((1%2Ff)+-+(1%2Fb))

bei Summe ist es 1/a = Nenner / Zähler >>> (d+e)/(b+c)

Bei deiner ersten Fkt kann man wegen der multiplikativen Verknüpfung rechts G und den Bruch für sich in den Kehrwert bringen.

Answer 2

[Per78]

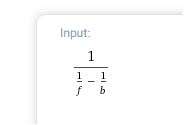
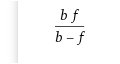
Du dividierst die Zahl oder wovon auch immer du den Kehrwert brauchst durch 1. (Manche Taschenrechner haben sogar eine [1/x]-Taste im den Kehrwert schnell zu berechnen.)

Bei einem Bruch musst du nur Zähler und Nenner vertauschen. Zb ist der Kehrwert von 5/3 = 3/5

Die Umformung der Linsengleichung findest du hier:

https://lernvorsprung.at/linsengleichung-umformung-zur-brennweite/

Comments

[Volens]

Du dividierst 1 durch die Zahl, um den Kehrwert zu bilden.

[Per78]

@Volens

hehe ja, stimmt... sorry :D

Answer 3

[MatthiasHerz]

Grundsätzlich bekommst den Kehrwert, indem durch den Zähler teilst und mit dem Nenner multiplizierst …

x = 3/4 | : x : 3 • 4

<=> 4/3 = 1/x

Analog dazu ist der Kehrwert der fraglichen Summe …

1/a = (d + e) / (b + c)

… und weiter durch Multiplikation mit den Nennern …

<=> b + c = a (d + e)

… abzüglich c …

<=> b = a (d + e) - c

Genau das gleiche für die Differenz …

1/g = 1/f - 1/b

… wo hier als Kehrwert 1 / (1/f - 1/b) bekämest oder besser zuerst den Hauptnenner bildest …

<=> 1/g = (b - f) / (fb) | ( )⁻¹

<=> g = fb / (b - f)

Um nach b umzustellen, benötigst jedoch die Ausgangsgleichung, wo 1/f abziehst …

1/g - 1/f = (-1/b)

… den Hauptnenner bildest …

<=> (f - g) / (fg) = (-1/b)

… und dann den negativen Kehrwert …

<=> (-fg) / (f - g) = b