Mathematik --Integralrechnung?
Ich hab immer noch nicht ganz kapiert, wofür jetzt dx steht. Kann mir das bitte jemand erklären?
Mfg. Anja (13)
4 Antworten
"dx" ist Faktor. "dx" ist eine Infinitesimalzahl (keine reelle Zahl, keine komplexe Zahl, ..., eine ganz andere Menge von Zahlen), was man leider in der Schule nicht lernt. Man lernt zwar "Infinitesimalrechnung" als Zusammenfassung von Differential- und Integralrechnung, aber nicht was das genau Bedeutet.
SchuleIn der Schule lernt man in der Regel:
df(x) = f(x + dx) - f(x)
Dabei lernt man "dx" definiert durch:
(simplifiziert)
In Wirklichkeit ist "dx" eine Differenz zweier x-Werte, die wir gegen 0 laufen lassen, aber die 0 ist.
aka als eine Zahl die "unendlich" nahe an 0 ist. Und diese Art von Zahlen hat sehr coole Eigenschaften. Sich das vorstellen kann jedoch schwer sein. Man wird an sie herangeführt über Ableitungen, wo man den Übergang von Differenzenquotient zum Differentialquotient lernt.
BeispielWir wissen, dass wir die Durchschnittsgeschwindigkeit eines Autos berechnen können mit:
∆Geschwindigkeit = |Position 1 - Position 2| / |Zeit 1 - Zeit 2|
∆Geschwindigkeit = ∆Position / ∆Zeit
Wir erhalten die Durchschnittsgeschwindigkeit zwischen Position 1 und 2. Doch was ist wenn wir wissen wollen, wie schnell das Auto genau ist zu einen gewissen Zeitpunkt?
Es ist trivial, dass wenn wir ∆Zeit kleiner machen, wir der Frage immer näher kommen. Denn die beiden Positionen und die beiden Zeiten sich der Stelle annähern an der wir die genaue Geschwindigkeit wissen wollen.
Da können wir doch sagen, lass uns ∆Zeit "= 0" einsetzen, kleiner geht es schließlich nicht. Aber Division durch 0 ist nicht definiert also geht das nicht. Aber wir können ∆Zeit kleiner werden lassen. Sagen wir ∆Zeit = 0,1..., ∆Zeit = 0,01..., ∆Zeit = 0,001... Das was wir machen ist ∆Zeit gegen 0 laufen zu lassen. Das Ergebnis ist "dZeit".
"dx" ist also die Differenz zweier x-Werte ("∆x"), welche wir gegen 0 laufen lassen aber nicht 0 sein lassen.
ProblemeDas ist die Theorie. Doch des mehr man in die Theorie on verschieden Gebieten der Mathematik man geht, des Wager kann die Bedeutung von "dx" werden.
Z.B. in der fraktionellen Infinitesimalrechnung, weist die Definition aus der Schule viele Lücken auf, weswegen wir die Definition erweitern müssen, doch die Erwartungen variieren.
Wir können "dx" auch über "unendlich" große Zahlen definieren. Was sehr eigenartig wird, weil es sehr viele Arten von "Unendlichkeiten" und "unendlich großen Zahlen" gibt. Stichworte sind hier Transfinite Zahlen, Hyperreelle Zahle, Ordinalzahlen, Surreale Zahlen, Kardinalzahlen, ...
Joa. Vielleicht ist Anja mit 13 Jahren ein falscher Adressat für meine Antwort.
Aber er/sie/... hat bestimmt vieles interessantes in Antwort erfahren womit er/sie/... sich beschäftigen kann.
Wow, eine sehr ausführliche Erklärung, vielen Dank. Auch, dass sie sich die Zeit genommen haben es mir zu erklären. Ich habe es verstanden. Wissen sie in welcher Klasse man das normalerweise lernt?
Gerne.
Den Beginn davon, also da wo man "dx" das erste mal begegnet sollte in Deutschland Ende der 10 Klasse (Gymnasium) bzw. zu Beginn der 11 Klasse sein (Abitur).
Die genannten Probleme und die genannten Zahlenarten lernt man in der Regel nicht in der Schule kennen.
Komplexe Zahlen, Kardinalzahlen, Ordinalzahlen und transfinite Zahlen kann man in Studium kennen lernen.
Dankeschön. Ich versteh nicht, wieso man nicht wenigstens die komplexen Zahlen in der Schule lernt, wenn man sich mit Wurzeln befasst. Anstatt zu sagen es gibt keine Wurzel aus negativen Zahlen...
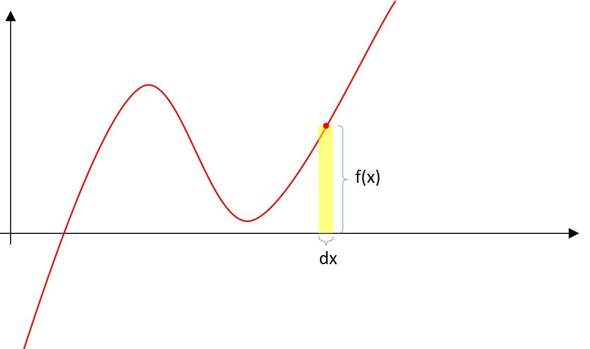
Bei der Integralrechnung geht es vornehmlich um die Berechnung von Flächen, die durch "krumme" Strukturen begrenzt sind, in einfachen Fällen um Flächen unter Kurven. Diese zerlegt man dann in kleine Rechtecke bzw. Streifen mit der Höhe f(x) und der Breite dx. dx ist somit einfach die Streifenbreite.
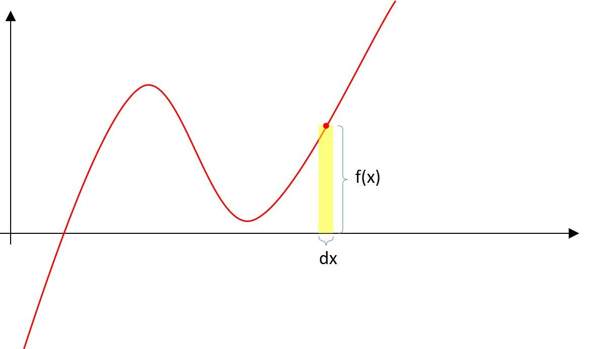
Oh, laut anderen Kommentaren ist dx ein unendlich kleines Intervall... Was stimmt nun?
dx wird unendlich klein. Man lernt in der zehnten bspw., dass man eine Sekante, die den Durchschnitt einer Steigung berechnet, auf möglichst einen x Wert kürzen kann bzw., dass man den Abstand zwischen zwei Punkten unendlich klein in x Richtung macht, so erfolgt: (f(x+h)-f(x))/h .Nun versucht man h möglichst klein, also gegen Null anstreben zu lassen.
Man kürzt dann h raus und hat dann die exakte Steigung der Gesamten Funktion in Abhängigkeit des x Werts.
Was ist das Integral ?
Es ist der Grenzwert von Riemannsummen
Int f dx = lim /pi / to 0 R(f,/pi ) die man vereinfacht als R ( f, /pi) = /sum fx_i * / delta x_i schreiben kann.
Bem: Bedeutung von dx hängt vom.Gebeit und der geforderten Genauigkeit ab..
Oh, okay.... Ob ich das verstanden habe weiß ich nicht...
Das Riemannintegral ist nach Definition der Grenzwert einer "Folge" (genauer gesagt eines Netzes) von Riemannsummen- die die Form
Summe f(t_i) * delta x_i
haben - wobei delta x gegen 0 ( in gewissem Sinne) und delta x --> 0 wird als dx bezeichnet.
Und der Unterschied in der Notation zwischen Riemannsummen ist im.wesentlichen
1) das man das Summensymbol durch das Integralsymbol.ersetzt
2) das delta x durch dx ersetzt
Ich empfehle Dir, das dx einfach als Schreibweise zu akzeptieren. Dahinter steckt die Theorie der Integration von Differentialformen. Das dx bzw. f dx ist eine sogenannte 1-Form…
Wenn du mein Beispiel oder meine Erzählart nicht magst dann kannst du eine alternative Herleitung zu einen ähnlichen Beispiel auf Wikipedia sehen: https://de.wikipedia.org/wiki/Differentialrechnung#Heranf%C3%BChrung_anhand_eines_Beispiels