[Mathe] Stochastik - Aufgabe mit Glücksrad richtig?
Guten Morgen,
habe ich die folgende Aufgabe richtig gelöst? Gibt es einen einfacheren Weg als meine Vorgehensweise?
So hat diese Aufgabe mein Mathelehrer in der Schule vorgerechnet:
Wieso weicht das Ergebnis von euren Ergebnissen ab? Wie genau hat mein Lehrer das gemacht und wieso steht hier die ganze Zeit „größer gleich“ und „kleiner gleich“? Gerne mit einer genauen Erklärung, wie er es gemacht hat und ob seine Rechnung richtig oder falsch ist.
Folgendes hatte er noch danach geschrieben und gesagt, es sei ein anderes Beispiel (Leider gestaltet mein Lehrer den Unterricht sehr unübersichtlich):
Hier ist meine richtige bearbeitete Aufgabe, habe ich leider gar nicht bemerkt, dass ich es noch nicht so gepostet habe:
3 Antworten
Hallo,
sieht gut aus. Allerdings ist die Wahrscheinlichkeit von mindestens 99 %, daß mindestens einmal die 2 erscheint, erst ab der neunten Serie von je zwei Drehungen gegeben, da Du nach acht Serien noch ganz knapp unter 99 % liegst.
Da n nur eine natürliche Zahl sein kann, muß die Antwort daher n=9 lauten.
Herzliche Grüße,
Willy
Es heißt doch mindestens 99 %. Bei 8 Spielen liegt die Wahrscheinlichkeit aber noch nicht bei 99 %, sondern knapp darunter. Um über die 99 %-Marke zuu kommen, mußt Du noch ein neuntes Spiel machen.
Das sind natürlich statistische Werte. Du kannst auch Glück haben und nach dem 20. Spiel immer noch keine 2 gedreht haben. Es kann auch gleich beim ersten Spiel rappeln. Auf lange Sicht aber steigt die Wahrscheinlichkeit, das Spiel zu verlieren, ab neun Runden auf über 99 %.
Stimmt, bei 8,00392278 beträgt die Wahrscheinlichkeit genau 99 %. Und wir möchten ja herausfinden, bei wie vielen Spielen die Wahrscheinlichkeit für mindestens ein verlorenes Spiel bei über 99 % liegt. Also:
Ab dem 9. Spiel liegt die Wahrscheinlichkeit für mindestens ein verlorenes Spiel bei über 99 %.
Aber der Spieler kann doch nur 8 mal spielen, bevor die Wahrscheinlichkeit über 99 % für ein verlorenes Spiel beträgt? War das nicht die Frage?
Schon bei zwei Runden steigt die Wahrscheinlichkeit zu verlieren auf über 2/3, bei vier Runden auf knapp 90 %.
Habe meinen vorherigen Kommentar gerade nochmals bearbeitet
So gesehen hast Du recht. Ab dem neunten Spiel steigt die Wahrscheinlichkeit auf über 99 %, bis zum achten Spiel liegt sie darunter. Ich hatte mir die Frage nicht ganz genau durchgelesen. Dann bleibt es bei n=8.
Schon bei zwei Runden steigt die Wahrscheinlichkeit zu verlieren auf über 2/3, bei vier Runden auf knapp 90 %.
Das kann doch nicht sein, oder?
A: Wahrscheinlichkeit zu verlieren (mindestens eine 2)
A = {24; 42; 22}
P(A) = 0,25*0,75+0,75*0,25+0,25*0,25
P(A) = 0,4375 = 43,75 %
Bei zwei Runden steigt die Wahrscheinlichkeit zu verlieren doch nicht über 2/3.
Ah, ich habe nur ein Spieldurchlauf betrachtet. Was fehlt noch bei meiner Rechnung?
Da zweimal gedreht wird, ist die Wahrscheinlichkeit für keine 2 (3/4)²=9/16.
Bei zwei Runden sinkt die Wahrscheinlichkeit zu gewinnen auf (9/16)²=0,316. Damit steigt die Wahrscheinlichkeit zu verlieren auf über 68 %, also auf über 2/3.
Wie hätte ich das mit meiner Rechnung zu Ende rechnen können? Ich habe ja P(A) = 43,75 % berechnet.
1-(9/16)², ganz einfach. Das wäre die Wahrscheinlichkeit, bei zwei Runden zu verlieren.
Das habe ich verstanden, aber ich habe ja schon die Wahrscheinlichkeit bei einer Runde zu verlieren, berechnet. Kann ich nicht einfach mit P(A) = 0,4375 = 43,75 % weiter rechnen? Wieso kann ich dann nicht einfach 0,4375^2 rechnen?
Die Wahrscheinlichkeit zu verlieren steigt doch mit der Anzahl der Runden an. Mit Deiner Rechnung kämst Du aber auf immer kleinere Werte. Das würde bedeuten, daß Du bei 100 Runden mit größerer Wahrscheinlichkeit immer gewinnen würdest als bei einer. Das kann nicht sein.
Es ist ja auch nicht wahrscheinlicher, zweimal hintereinander einen Sechser im Lotto zu haben als einmal. Umgekehrt wird ein Schuh daraus.
Da hast Du recht. Bis achtmal geht alles gut (mit einer Wahrscheinlichkeit von etwas über 1 % natürlich nur). Ab dem neunten Spiel sinkt die Wahrscheinlichkeit, alle diese neun Spiele zu gewinnen, auf unter ein Prozent.
Hey Willy, ich brauche dringend Hilfe bei dem Verständnis von den Funktionen „sum(“, „Binomialpdf“ und „Binomialcdf“ im Taschenrechner bei Stochastik und habe gerade eine Frage dazu gepostet. Es würde mich wirklich sehr glücklich machen, es endlich zu verstehen und mir sehr weiterhelfen. Vielleicht magst du dir ja meine Frage ansehen: https://www.gutefrage.net/frage/koennt-ihr-mir-diese-wtr-funktionen-fuer-stochastik-erklaeren
Liebe Grüße
maennlich2002
Vielen Dank für den Stern.
Mit ti-Rechnern kenne ich mich überhaupt nicht aus.
Vielen Dank für deine Hilfe. Vielleicht kennst du dich ja mit der Binomialverteilung in Mathe aus und magst mir bei meiner neuesten Frage weiterhelfen: https://www.gutefrage.net/frage/was-ist-mein-denkfehler-bei-der-binomialverteilung
Hey, schau dir bitte die Ergänzung der Frage an und gebe mir dazu bitte ein Feedback :) Mein Lehrer kam auf das Ergebnis, dass man nur fünfmal spielen kann und beim 6. Spiel P über 0,99 liegt.
Das ist die Wahrscheinlichkeit dafür, daß mindestens ein Spiel mit einer Wahrscheinlichkeit von über 99 % gewonnen wird. Danach war aber in der Aufgabe gar nicht gefragt.
Kannst du das nochmal bitte ganz genau erklären? Ich stehe gerade einfach auf dem Schlauch. Gesucht ist ja die Anzahl der Spiele, die ein Spieler spielen kann, bevor die Wahrscheinlichkeit für ein verlorenes Spiel über 99 % liegt. Wer hat nun falsch gerechnet? Ich oder mein Lehrer? Wie hat es mein Lehrer gemacht, was genau hat er gemacht? Das würde mir sehr helfen :)
Deine Rechnung ist richtig. Die Wahrscheinlichkeit dafür, daß alle Spiele gewonnen werden, muß auf unter 0,01 sinken, dann ist im Gegenzug die Wahrscheinlichkeit für mindestens ein verlorenes Spiel auf über 0,99 gestiegen.
Du rechnest 1-(9/16)^n>0,99 und das ist bei n>8 der Fall.
Habe die Frage nochmals ergänzt, aber auch dort ist für Berechnung bzw. die Interpretation meines Lehrers falsch, oder? Ich würde gerne die genaue Vorgehensweise meines Lehrers komplett verstehen, um in Zukunft solche Aufgaben, bei denen n gesucht ist, gut lösen zu können. Vielleicht magst du mir da ja mal die Vorgehensweise meines Lehrers ganz genau erklären. Das würde mir unglaublich viel helfen. 🙏
Hey Willy,
schau dir sehr sehr gerne meine neueste Frage an :-) Es geht auch um Wahrscheinlichkeit, immer noch um das Glücksrad, nur eine andere Fragestellung: https://www.gutefrage.net/frage/wahrscheinlichkeit-beim-gluecksrad-und-werte-fuer-x
Liebe Grüße
maennlich2002
Guten Abend, schau dir sehr gerne meine neueste Frage an: https://www.gutefrage.net/frage/wahrscheinlichkeitsaufgabe-nationale-anti-doping-agentur. Das würde mir wirklich sehr helfen :-)
Meiner Meinung nach sind beide Ansätze falsch (viel zu kompliziert gedacht) und bei dir ist zusätzlich ein Rechenfehler drin.
Die Aufgabe ist sehr einfach zu lösen. Sie entspricht der Aufgabe "Kugeln ziehen mit zurücklegen".
Die Ereignisse finden nacheinander statt, daher dieser Ansatz, den du auch verwendest, bloß nicht korrekt durchgeführt hast.
Den Rechengang und den Ansatz vom Lehrer kann ich nicht nachvollziehen.
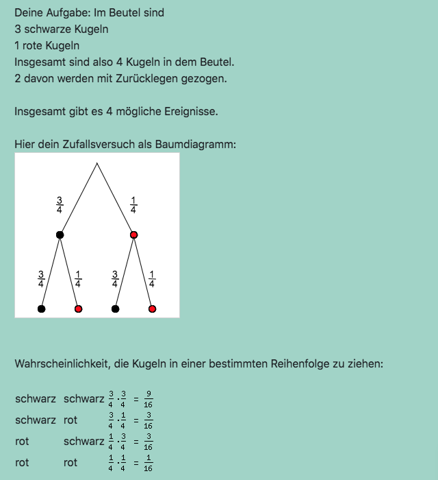
Nehmen wir an, wir haben kein Glücksrad, sondern einen Beutel und nicht 3 Felder mit 4, sondern 3 scharze Kugeln und nicht 1 Feld mit 2, sondern eine rote Kugel.
Dann sieht bei einem Spiel das Baumdiagramm so aus:
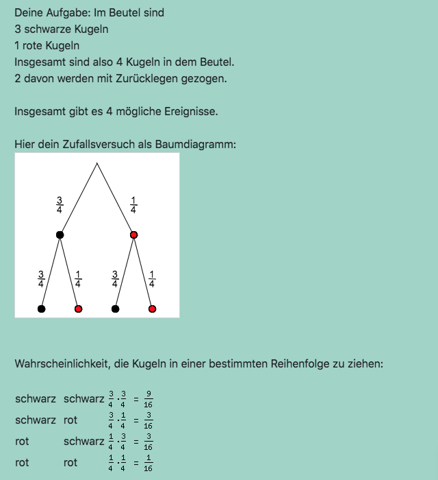
Die Wahrscheinlichkeit, dass keine 2 kommt, liegt also bei 9/16.
Bei 2 Spielen hintereinander liegt die Wahrscheinlichkeit, keine 2, also immer nur 4 zu kriegen, bei (9/16)^2 etc.
Nun berechnen wir, wie oft man ziehen muss, um auf p = 0,01 zu kommen:
0,01 = (9/16)^n
und lösen nach n auf:
ln 0,01 = ln (9/16)^n
ln 0,01 = n * ln (9/16)
n = ln 0,01 / ln (9/16) = 8,004
Nun kommt der Fehler: man darf nicht runden. 8 würde die Aufgabe noch nicht erfüllen, da wäre p knapp kleiner als 99 %. Erst bei 9 ist sie höher.
Habe die Frage gerade (vor ca. 10 Minuten) nochmals um eine Ergänzung ergänzt, vielleicht magst du dir sie ja auch noch ansehen und darauf eingehen 🙏
Nun ja, dann kommt er jetzt ja zum selben Ergebnis...aber viel komplizierter als notwendig.
Vielen liebe dank fürs Anschauen! :-) Wie genau mein Lehrer da vorgegangen ist, kannst du mir bestimmt nicht erklären, oder?
Vielleicht ist seine komplizierte Vorgehensweise ja bei anderen Aufgaben notwendig, wofür ich diese Vorgehensweise dann womöglich beherrschen muss.
Vielleicht ist seine komplizierte Vorgehensweise ja bei anderen Aufgaben notwendig, wofür ich diese Vorgehensweise dann womöglich beherrschen muss.
Das kann sehr gut sein.
Habe die Frage nochmals ergänzt (um meine aktuelle Version der bearbeiteten Aufgabe, hatte ich leider gar nicht gemerkt).
und lösen nach n auf:
ln 0,01 = ln (9/16)^n
ln 0,01 = n * ln (9/16)
n = ln 0,01 / ln (9/16) = 8,004
Nun kommt der Fehler: man darf nicht runden. 8 würde die Aufgabe noch nicht erfüllen, da wäre p knapp kleiner als 99 %. Erst bei 9 ist sie höher.
Ich bin doch auch auf ≈ 8,0039 gekommen und habe dann als Antwort geschrieben:
Ein Spieler kann 8-mal „keine Zwei“ spielen, bevor die Wahrscheinlichkeit für mindestens ein verlorenes Spiel bei über 99 % liegt.
Wo ist mein Rechen/Denk - Fehler? 🤔
um auf genau 99 % zu kommen, muss er 8,004 mal spielen. Bei 8 mal bleibt er dann knapp unter den 99 % und damit wäre die Aufgabe nicht erfüllt. Die nächste natürlich Zahl nach 8,003 wäre 9. Damit kommt er dann über 99 %.
Aber die Frage ist doch, wie oft ein Spieler „keine Zwei“ spielen kann, bis die Wahrscheinlichkeit für mindestens ein verlorenes Spiel über 99 % liegt. Also so oft er spielen kann, bevor die Wahrscheinlichkeit bei über 99 % liegt, oder? So habe ich das verstanden. Und ich habe es doch ganz genau in der Antwort geschrieben, oder nicht:
Ein Spieler kann 8-mal „keine Zwei“ spielen, bevor die Wahrscheinlichkeit für mindestens ein verlorenes Spiel bei über 99 % liegt
?
Denn beim neunten Spiel liegt die Wahrscheinlichkeit doch bereits bei über 99 %. Gefragt ist doch die Anzahl der Spiele, die ein Spieler „keine Zwei“ spielen kann, bis die Wahrscheinlichkeit für mindestens ein verlorenes Spiel über 99 % liegt. Vielleicht stehe ich auch einfach auf dem Schlauch… Ich würde immer noch sagen, dass meine Antwort richtig ist 🤔 Weil ich es einfach nicht verstehe, wieso es anders ist.
Ja, stimmt. Habe das schneller und anders gelesen..."..ab wann steigt die Wahrscheinlichkeit über 99 %".
Hallo,
du hast mit 9/16 gerechnet, dein Lehrer mit 1 - 9/16=7/16.
Der Aufgabentext ist ziemlich verdreht.
Die Wahrscheinlichkeit für ein gewonnenes Spiel ist 9/16. Die Wahrscheinlichkeit n Spiele hintereinander zu gewinnen beträgt (9/16)^n, die Gegenwahrscheinlichkeit also 1-(9/16)^n≥0,99.
...
Der Fehler im Rechenweg sieht meiner Meinung nach so aus:
Statt P(X≥1) müsste es P(X<n) heißen.
P(X=n) bedeutet ja, dass alle n Spiele gewonnen werden. P(X<n) heißt entsprechend, dass mindestens eins verloren wurde.
Vielen Dank für deine Antwort. Wenn du noch Lust hast mir zu helfen, kannst du dir sehr gerne meine zwei neuesten Fragen ansehen - das würde mir unglaublich viel helfen, wenn du mir darauf eine Antwort geben würdest. 🤓.
So ganz verstehe ich es leider noch nicht, wieso hier die Antwort n = 9 lauten muss. 🤔 Kannst du mir das vielleicht nochmal genau erklären wo genau die Differenz ist?