Mathe Körper und Flächen?
Kann mir einer vielleicht diese aufgabe machen, ich komme nicht weiter😭wäre echt lieb
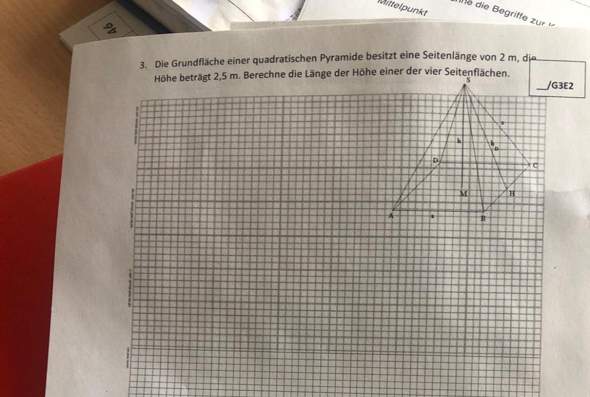
2 Antworten
Nutzer, der sehr aktiv auf gutefrage ist
Das Dreieck MHS ist ein rechtwinkliges Dreieck. Es folgt:
hD²= (a/2)² + h²
Ziehen der Wurzel liefert das gesuchte Ergebnis:
hD = sqrt((a/2)² + h²)
wobei sqrt(...) die Wurzel bezeichnet.
RipedimeActing
15.04.2024, 21:54
@Peter36119
Er rechnet das ganze über a^2+b^2=c^2. a entspricht hier a/2, also der Kantenlänge der Grundfläche durch 2, b entspricht h und damit der Höhe der Pyramide und c entspricht hD, also der Länge der dritten Dreiecksseite.
@RipedimeActing
Also nach ddm wurzeln ziehen muss ich als lösung 2,69 schreiben oder?
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik, rechnen, Funktion
Gesucht: Seitenhöhe hD
Gegeben: a = 2 m
Gegeben: h = 2,5 m
---
hD = Wurzel( h² + (a/2)² )
hD = Wurzel( 2,5^2 + (2/2)^2 )
Seitenhöhe hD beträgt 2,692582 m
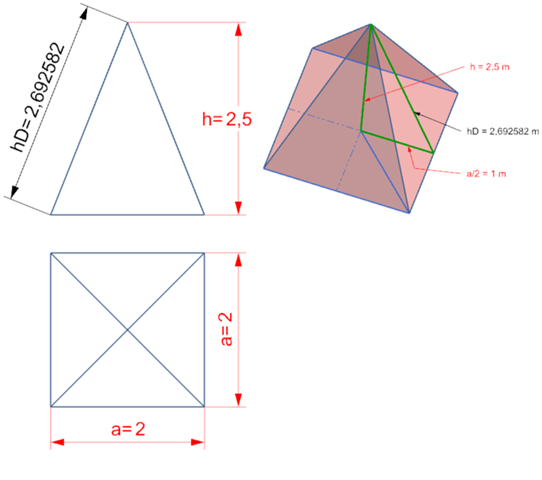
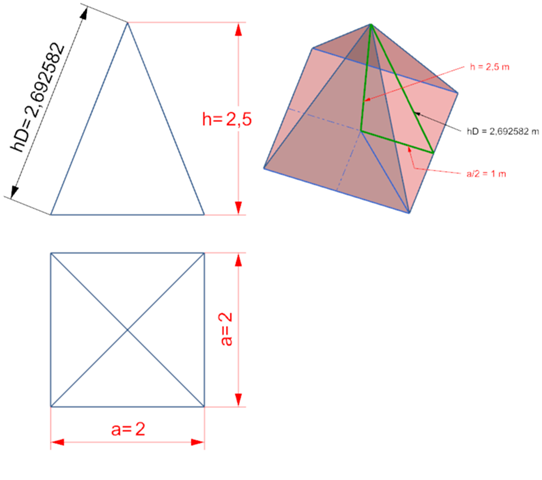
Viel zu schwer erklärt 😭