Wie berechne ich die Fläche?

Hey,

Ich komme bei dieser Aufgabe einfach nicht weiter. Ich hoffe ihr könnt mir helfen. Wir berechne ich die Fläche von dem Teil?

Answer 1

[merkurus]

Aufgabe 4
Fläche A1 (2x)
A1 = ((a * c) - ((r^2 * PI()) / 2))
A1 = ((9 * 3) - ((2,5^2 * PI()) / 2))
A1 = 1146,570826 * 2
A1 = 17,18252296 cm²
---
Fläche A2 (2x)
A2 = b * c
A2 = 6 * 3
A2 = 18 cm²
---
Fläche A3 (2x)
A3 = d1 * b
A3 = 2 * 6
A3 = 12 cm²
---
Fläche A4 (1x)
A4 = (r * 2 * pi / 2) * b
A4 = (2,5 * 2 * pi() / 2) * 6
A4 = 47,12389 cm
---
Fläche A5 (1x)
A5 = a * b
A5 = 9 * 6
A5 = 54 cm²
---
Oberfläche Gesamt
A = (A1 * 2) + (A2 * 2) + (A3 * 2) + A4 + A5
A = (17,18252296 * 2) + (18 * 2) + (12 * 2) + 47,12389 + 54
A = 195,4889359 cm²

Answer 2

[Peppie85]

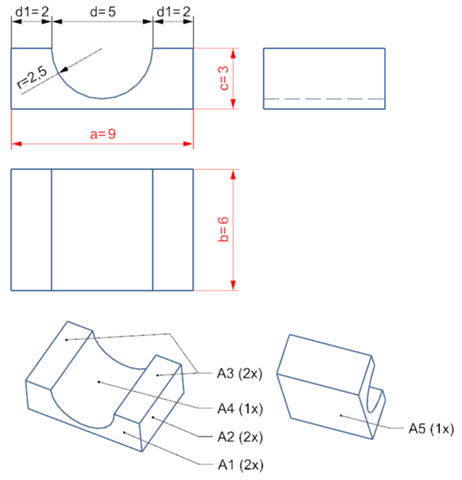
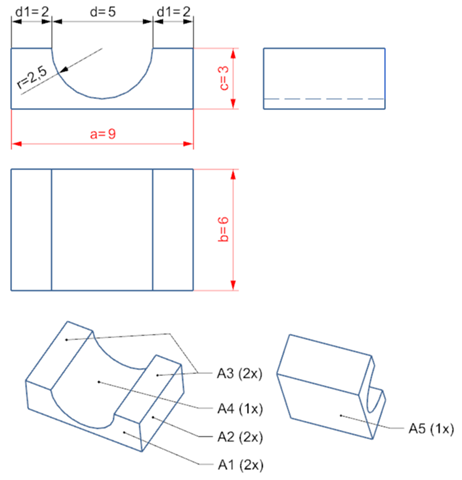
Fangen wir einfach mit dem Quader als Grundkörper an. 9 x 6 x 3 cm. Damit haben wir schon das Volumen des Grundkörpers.

von der Ausparung nehmen wir mal an, es wäre ein Halbkreis. wir gehen auch mal davon aus, dass der Körper symetrisch ist. d.h. links ist die kleine fläche ebenfalls 2 cm.

jetzt brauchst du nur noch das volumen des halbzylinders zu berechnen und von dem des Grundkörpers abzuziehen

die Fläche eines Kreises kansnt du nach

$A=\frac{d^2\cdot\pi}{4}$ oder

$A=R^2\cdot\pi$ ausrechnen.

das Ganze noch mal die Höhe des Zylinders in dem fall 6 cm und eben halbiert. schon hast du das Volumen des Halbzylinders.

für die Fläche würde ich einfach den vollkreis nehmen. und das Ergebnis, das du ja schon hast, von der vorderen und hinteren Fläche gemeinsam, hier 54 cm² abziehen.

dann musst du nur noch die Kontur außenrum nehmen. also 2 + X + 2 + 3 + 9 + 3 cm und mit der tiefe der Figur von 6 cm malnehmen.

X ist dabei die Länge des Halbkreises. Dafür einfach Durchmesser mal pi und das halbieren...

lg, Anna

Answer 3

[PatrickOm]

Ich habe es mir kurz angesehen.

Die totale Lösung kann ich dir hier nicht präsentieren, denn dafür ist GF wahrscheinlich nicht da.

Aber einen Lösungsansatz:

Einige Oberflächen sind ja einfache Rechtecke. In der vorderen und hinteren Fläche befindet sich ein Halbkreis, der mit einem Schnitt in seiner Hälfte ja auch genau definiert ist. Diesen dann abziehen. Und das Runde ist die Hälfte einer Außenfläche eines Zylinders.

Woher ich das weiß: eigene Erfahrung

Comments

[Philanus]

Was meinst du mit GF? :)

Philanus

[PatrickOm]

@Philanus

Gute Frage. Wird hier oft als Kürzel benutzt. 😀

[Philanus]

@PatrickOm

Ich dachte, du meinst ein mathematisches Verfahren, von dem ich noch nichts gehört habe. :D

[PatrickOm]

@Philanus

Ah so, ok 😀

[Wernda12]

Okay. Danke schonmal.

Also ich denek ich kann bei dem Teil nicht das gesamte reckteck berechnen und dann einen halben zylinder abziehen oder?

[PatrickOm]

@Wernda12

Also, ich probier es mal so:

2 Seiten- , 2 obere Flächen + 1 Unterfläche mit den sich ergebenden Maßen berechnen.

Vorder- und Hinterfläche mal als Gesamtfläche berechnen, ohne den durchlöchernden Kreis.

Dann den Kreis mit Radius bzw Durchmesser berechnen. Diesen als ganzen Kreis (nämlich 2 Hälften) von den beiden Vorderflächen addiert abziehen.

Dann die Oberfläche des runden Teils des Zylinders berechnen (Grundfläche mal Höhe , also ganzer Kreis mal Höhe).

Die Hälfte dieser Oberfläche dann zu der bisherig berechneten Gesamtfläche addieren.

Ich bin eher nur ein Hobby-Mathematiker, aber vielleicht kann das helfen 😀🤔.

Answer 4

[evtldocha]

Das ist ein Quader minus ein Halbzylinder der den Radius (9 - 4) / 2 cm hat.

Comments

[Wernda12]

Ja aber so kann man das doch garnicht rechnen oder?

[evtldocha]

@Wernda12

Das kann man schon, denn sonst hätte ich die Antwort nicht in der Form geschrieben. Man muss nur überlegen, welche Flächen man von der Fläche des Quaders erst abziehen muss, um anschließend die Fläche der Innenseite des Halbzylinders wieder zu addieren.