Logarithmus, lg Aufgabe?
leider verstehe ich die Aufgabe nicht ganz, die wir ohne Taschenrechner lösen sollen. Ich kann’s zwar mit den Logarithmen Gesetzen zu einem Bruch zusammenfassen, komm aber grad einfach nicht darauf, wie man das dann umformen/kürzen/lösen kann. Hat jmd eine Idee?
3 lg12 - lg3 + 6 lg5 - lg9 = lg 12^3*5^6/27
2 Antworten
Denke an die folgenden Rechenregeln für Logarithmen...

Im Fall b = 10, also für den dekadischen Logarithmus lg = log₁₀, erhält man dementsprechend...

Im konkreten Fall dann...

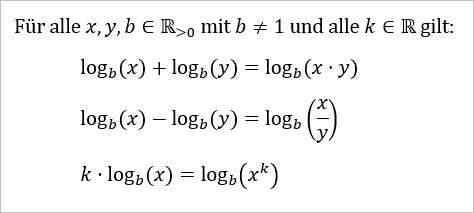
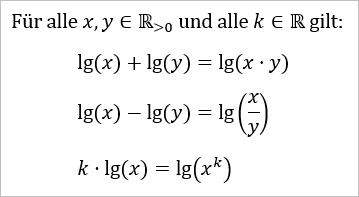

Ausgehend davon, wie weit du bereits umgeformt hast, kann man folgendermaßen weiterrechnen...
https://i.imgur.com/tQWGoO7.png
Im Grunde habe ich dabei die 12 in 2² ⋅ 3 zerlegt, die entsprechende Potenz auseinandergezogen und 3³ = 27 gekürzt. Schließlich habe ich das noch weiter zu 10^6 vereinfacht, was dann mit dem „lg“ davor schließlich 6 ergeben hat.
Bzw. hätte ich selbst die Aufgabe wohl folgendermaßen gelöst...
Wobei mir gerade aufgefallen ist...
Ich kann’s zwar mit den Logarithmen Gesetzen zu einem Bruch zusammenfassen, komm aber grad einfach nicht darauf, wie man das dann umformen/kürzen/lösen kann.
Demnach wird es also so sein, dass die Umformung...
3 ⋅ lg(12) - lg(3) + 6 ⋅ lg(5) - lg(9) = lg(12^3 ⋅ 5^6/27)
... gar nicht dein Problem ist, sondern das du danach nicht weiterkommst.
Da hatte ich nicht genau genug gelesen. Ich schreibe gleich nochmal was dazu. Moment...
Verwende die Rechenregeln für Logarithmen:
https://www.frustfrei-lernen.de/mathematik/logarithmus-regeln.html
Ach so, hast du ja schon gemacht. Nun die 3 aus der 12 raus ziehen und kürzen. Dann ist auch bei mir Ende...
Wie kann man das aber nun umformen, dass ohne TR 6 rauskommt?